Panduan Materi Belajar

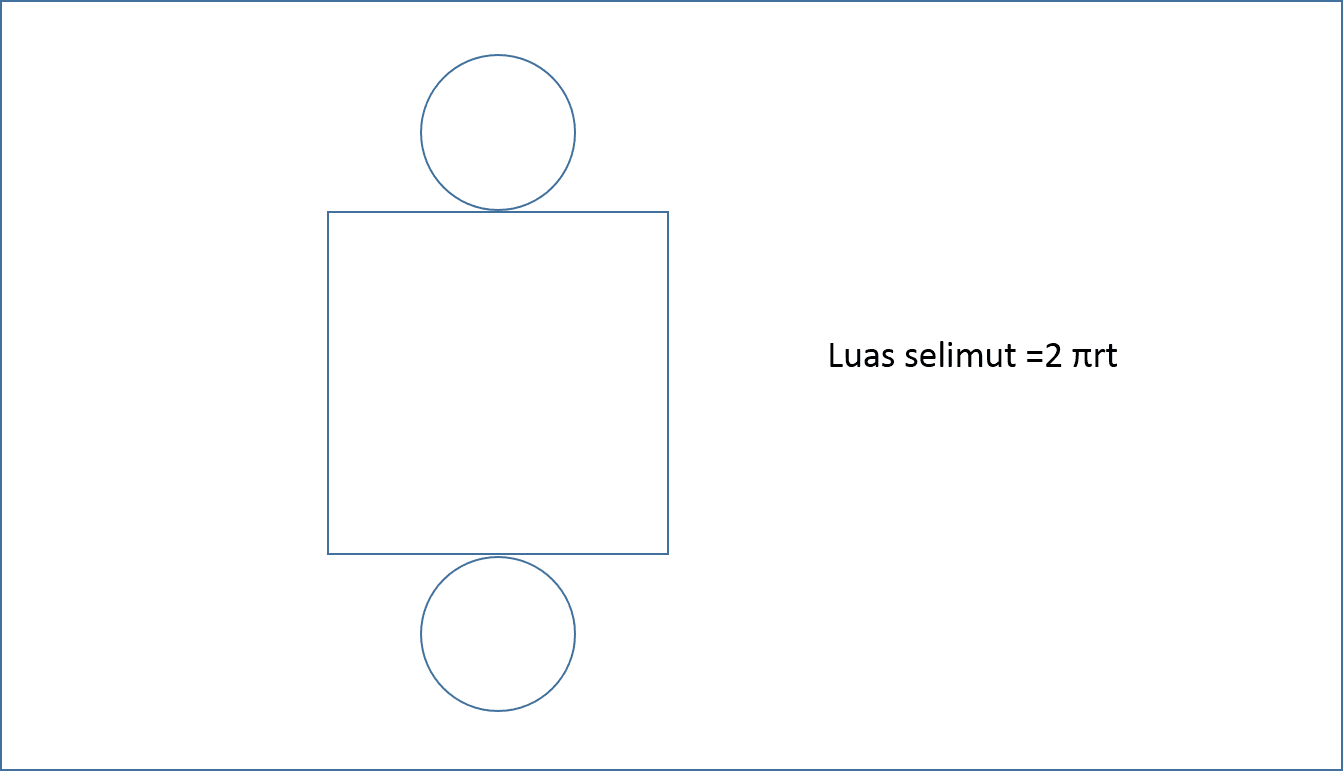
Karena diketahui luas selimut, maka data ini akan dipakai buat menemukan unsur yg belum diketahui. Masih jangan lupa menggunakan rumus selimut tabung? Mari kita kerjakan soalnya.. Contoh soal : 1. Sebuah tabung mempunyai luas selimut 880 cm² serta tingginya 10 cm. Berapakah volumenya? (π = ²²/₇) Diketahui dalam soal luas selimut = 880 cm² dan tinggi 10 cm. Kita gunakan rumus luas selimut buat mendapatkan jari-jari tabung, sebagai akibatnya volumenya sanggup dihitung. Luas selimut = 2πrt ganti luas selimut menggunakan 880 ganti tinggi dengan 10 880 = dua ײ²/₇ × r × 10 880 = ⁴⁴⁰/₇ × r untuk mendapatkan r, bagi 880 menggunakan 440 per 7 r = 880 : ⁴⁴⁰/₇ ubah tanda bagi sebagai kali dan 7 diatas sedangkan 440 dibawah. r = 880 × ⁷/₄₄₀ bagi 880 dengan 440 hasilnya2, kemudian kalikan menggunakan 7 serta hasilnya 14 r = 14 cm. Jari-jari sudah diperoleh, kini kita sanggup mencari volume dari tabung.. Volume tabung Volume tabung = πr² × t Volume tabung = ²²/₇ × 14² × 10 Volume tabung = 6160 cm³

Ok.. Sekarang kita akan mencari bagaimana cara mendapatkan luas bagian atas dari sebuah tabung yang diketahui volume serta tingginya. Karena nanti dalam soal diketahui volumenya, maka kita akan menggunakan donasi dari volume buat menerima data mengenai tabung yg belum diketahui. Biar lebih jelas, kita eksklusif kerjakan soalnya.. Soal : 1. Sebuah tabung diketahui volumenya 1570 cm³ dan tingginya lima cm. Berapakah luas permukaannya? (π = tiga,14) Pada tabung diatas, kita belum mengetahui jari-jarinya. Dan langkah pertama yang harus dilakukan adalah mencari berapa panjangnya. Mencari jari-jari (r) Kita akan menggunakan rumus volume buat membantu menemukan jari-jari menurut tabung ini. Volume tabung = πr²×t volume = 1570 t = lima cm π =  tiga,14 1570 = 3,14 × r² × 5 1570 = 15,7 × r² untuk menerima r², maka 1570 dibagi dengan 15,7 r² = 1570 : 15,7 r² = 100 untuk menerima r, akarkan 100 r = √100 r = 10 cm. Mencari luas bagian atas tabung Jari-jari telah diperoleh serta sekarang saatnya bu

Pada awalnya volume tabung telah diketahui, lalu tingginya dinaikkan menjadi dua kali menurut tinggi sebelumnya. Volume yang baru akan dicari. Bisa saja kita mencari tinggi awal dari tabung dulu lalu barulah dijadikan dua kali menurut semula, akan tetapi cara ini agak ribet. Atau sanggup dibilang rumit.. Mengingat nanti yang ketemu adalah tinggi yg mengandung variabel "r" atau jari-jari. Terkesan kurang sederhana.. Nanti kita akan memakai cara perbandingan, sebagai akibatnya prosesnya bisa dipermudah serta volumenya pribadi ditemukan. Soal : 1. Volume suatu tabung adalah 10 cm³. Apabila jari-jarinya permanen dan tingginya dinaikkan menjadi dua kali semula, berapakah volume tabung kini ? Ok, sebelumnya kita korek data-data yg sudah diberikan pada soal. Tabung mula-mula : Volume (V₁) = 10 cm³ jari-jari = r tinggi = t₁ = t Tabung setelahnya : Volume = V₂ (belum diketahui) jari-jari = jari-jari tabung pertama = r (jari-jarinya tetap, lihat dalam soal) tinggi = dua kali menurut t