Panduan Materi Belajar

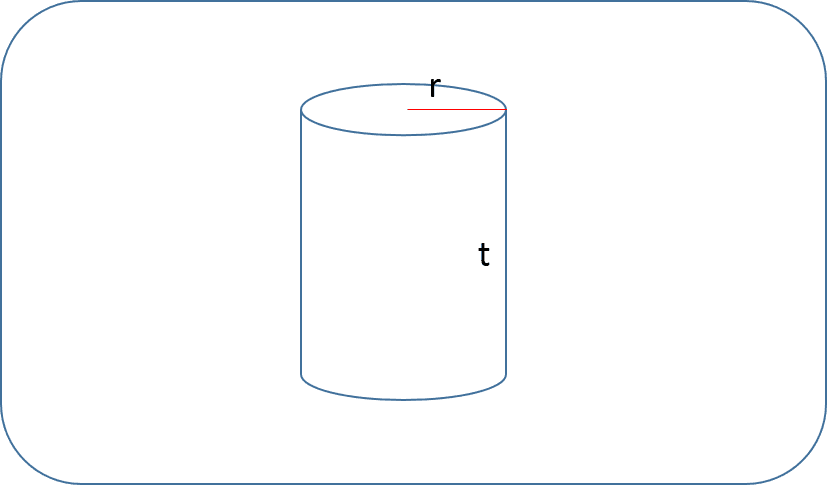
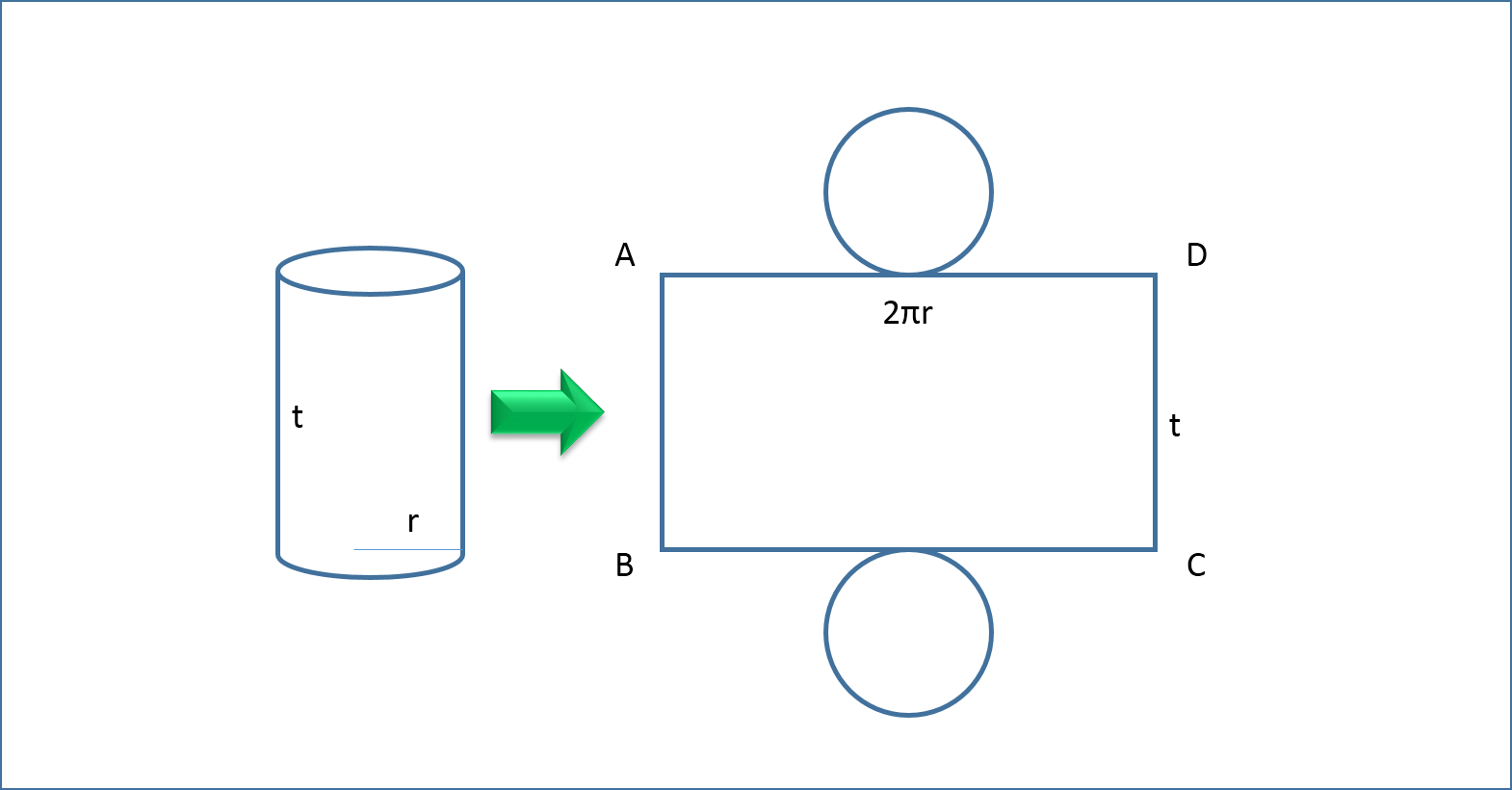
Karena yang diketahui adalah keliling alas serta jua tingginya, maka yg sebagai patokan kita pada memecahkan soal ini merupakan keliling alas. Ok, kita langsung saja cek soalnya ya.. Contoh soal : 1. Suatu tabung memiliki keliling alas 44 centimeter dan tinggi 10 centimeter. Berapakah volume dari tabung tadi? ( π = 22/7) Yuk kita cari jawabannya.. Langkah 1 => analisa soal Kita perhatikan yang diketahui : Keliling alas = 44 cm tinggi = 10 cm Dari apa yang diketahui, hanyalah keliling alas yang bisa dicari menggunakan memakai rumus. Keliling alas inilah yg akan sebagai titik awal kita buat mencari bagian lain yang belum diketahui pada tabung ini, yaitu jari-jari (r). Langkah 2 => Mencari jari-jari Keliling alas tabung berbentuk lingkaran, maka kita akan memakai rumus keliling dari bulat. Keliling alas = 2πr r = jari-jari Sekarang perhatikan perhitungannya.. Ganti nilai berdasarkan keliling dengan 44 π diganti menggunakan 22/7 Sekarang tinggal mencari r saja. Perhatikan baris pali

Masih ingat menggunakan volume tabung? Volume pada umumnya mengikuti rumus seperti ini = luas alas x tinggi. Sekarang buat bentuk tabung bagaimana? Ok,,, Tabung memiliki alas yang berbentuk bulat, berarti kita tinggal mencari luas berdasarkan lingkaran saja dulu. Inilah yg sebagai luas alasnya. Nah, ayo kita coba sedikit model soal  berikut adalah.. Contoh soal : 1. Sebuah tabung mempunyai jari-jari 7 cm serta tinggi 10 centimeter. Berapakah volume menurut tabung tersebut? Ok, gambar buat tabung mampu dipandang diatas.. r = jari-jari t = tinggi tabung Volume tabung = luas alas x tinggi. Luas alas tabung berbentuk bulat, berarti kita wajib memakai rumus menurut luas bulat lebih dahulu. Luas alas = luas lingkaran = π × r² Sehingga volume tabung menjadi : Volume = luas alas × tinggi Volume = π × r² × t Dalam soal sudah diketahui : r = 7 cm t = 10 cm Sekarang tinggal tambahkan seluruh ke rumusnya.. Oh ya, nilai berdasarkan π = ²²/₇, karena jari-jarinya kelipatan dari 7. Volume tabung = π

Cara yang baik buat mencari luas suatu bangun ruang adalah dengan membelah bangun tersebut. Kemudian dipecah-pecah serta dicari satu-satu. Dengan ini, kita akan sebagai lebih mudah mengerti dalam mencari rumus luasnya. Contoh soal Mari perhatikan contoh soal dibawah ini.. Contoh soal 1. Sebuah tabung memiliki jari-jari alas 7 centimeter dan tinggi 10 centimeter. Berapakah luas seluruh permukaan tabung tadi? Nah, perhatikan langkah demi langkah dalam merampungkan soal ini.. Langkah 1 => analisa soal Tabung bila dibelah, maka akan membuat misalnya gambar diatas. Tabung terdiri menurut : 2 butir bulat, alas serta tutup Selimut dengan panjang "2πr" dan berbentuk persegi panjang, lebarnya adalah tinggi tabung (t). Jadi buat mencari luas total tabung, tinggal jumlahkan saja ke-tiga bangun tersebut dan ketemulah luasnya. Untuk luas selimut bagaimana? Selimut tabung berbentuk persegi panjang : panjangnya sendiri sama menggunakan keliling lingkaran (2πr ).  Lebarnya sama dengan ti

Mencari volume bola yang berada dalam sebuah kubus sanggup dikerjakan dengan gampang bila telah mengerti triknya. Bagaimana triknya? Nah, kita lihat dulu soalnya serta selesainya itu akan saya jelaskan bagaimana trik gampang dalam menuntaskan soal ini.. Baca pula : Mencari tinggi kubus jika diketahui volumenya dua/tiga bagian Mencari volume kubus pada satuan liter Cek soal Yuk baca dulu soalnya!! Contoh soal : 1. Sebuah bola sempurna  memenuhi sebuah kubus. Jika panjang rusuk berdasarkan kubus tersebut 20 centimeter, berapakah volume bola maksimum yang mampu ditampung kubus? Nah, soalnya misalnya diatas... Sekarang saatnya untuk mencari jawabannya.. Langkah 1 ⇒ Analisa soal Perhatikan gambar diatas.. Volume bola maksimum yang mampu ditampung oleh kubus diatas terjadi jika diameter bundar sama dengan rusuk kubus. Nah, inilah trik pentingnya ya.. Trik penting!! Volume maksimum dicapai bila "diameter bola = rusuk kubus" Jadi diameter bola telah kita peroleh, yaitu sama mengguna

Nah, kali ini adalah deretan berdasarkan 2 butir bangun ruang. Dan sekarang ceritanya akan dimasukkan beberapa bola dengan berukuran eksklusif ke pada tabung yg mempunyai ukuran tertentu jua. Jangan resah dulu.. Nanti akan dijelaskan cara-caranya serta andapun niscaya akan mengerti menggunakan mudah.. Lihat soalnya Pertanyaan yg herbi perkara ini merupakan sebagai berikut.. Contoh soal : 1. Suatu tabung mempunyai diameter 12 centimeter dan tinggi 9 cm. Ke dalam tabung ini akan dimasukkan beberapa butir bola yang memiliki jari-jari 3 centimeter. Berapakah poly bola yg sanggup masuk ke pada tabung tadi? Mari kita analisa dulu soalnya.. Langkah 1 ⇒ Analisa soal Tujuan primer menurut soal ini merupakan mencari berapa poly bola yg masuk ke dalam tabung. Mudah sekali.. Benar sangatlah gampang.. Untuk menerima berapa poly bola yg bisa masuk ke dalam tabung, caranya merupakan dengan membagi volume yg lebih akbar menggunakan volume yang lebih mini . Volume lebih besar merupakan tabung Volume l

Rumus Volume serta Luas Permukaan Bola Beserta Contoh Soal - Bangun ruang Matematika terbagi menjadi beberapa jenis. Salah satunya adalah bangun ruang Bola. Bangun ruang ini bahkan tak jarang kita jumpai disekeliling kita. Bentuknya yang bundar menciptakan seluruh orang mengenalnya. Selain itu bangun ruang bola jua seringkali digunakan menjadi soal ujian sekolah. Maka berdasarkan itu buat menghitung model soal bola diharapkan rumus volume bola dan rumus luas permukaan bola yg sesuai. Dengan rumus tersebut maka anda dapat mengerjakan soal soal yang terdapat menggunakan benar. Bola adalah bangun ruang 3 dimensi yang mempunyai bentuk bulat. Permukaan pada bola mempunyai jeda yg sama menggunakan titik pusatnya. Bangun ruang ini nir memiliki titik sudut maupun rusuk. Jumlah sisinya saja hanya satu yaitu dinding bola. Pada kesempatan kali ini saya akan menjelaskan mengenai rumus volume bola serta rumus luas permukaan bola bersama contoh soal bola. Untuk detail bisa anda simak di bawah ini.