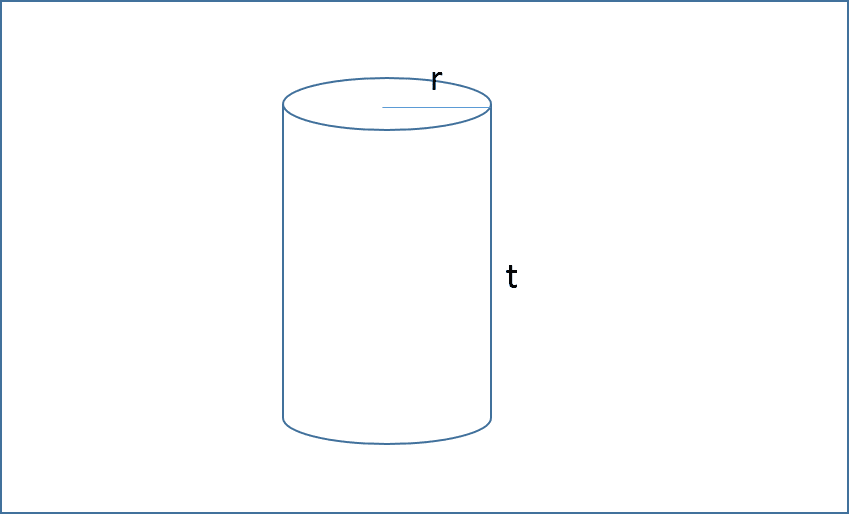
Mencari Luas Permukaan Tabung Jika Diketahui Jarijari dan Tingginya Terbaru
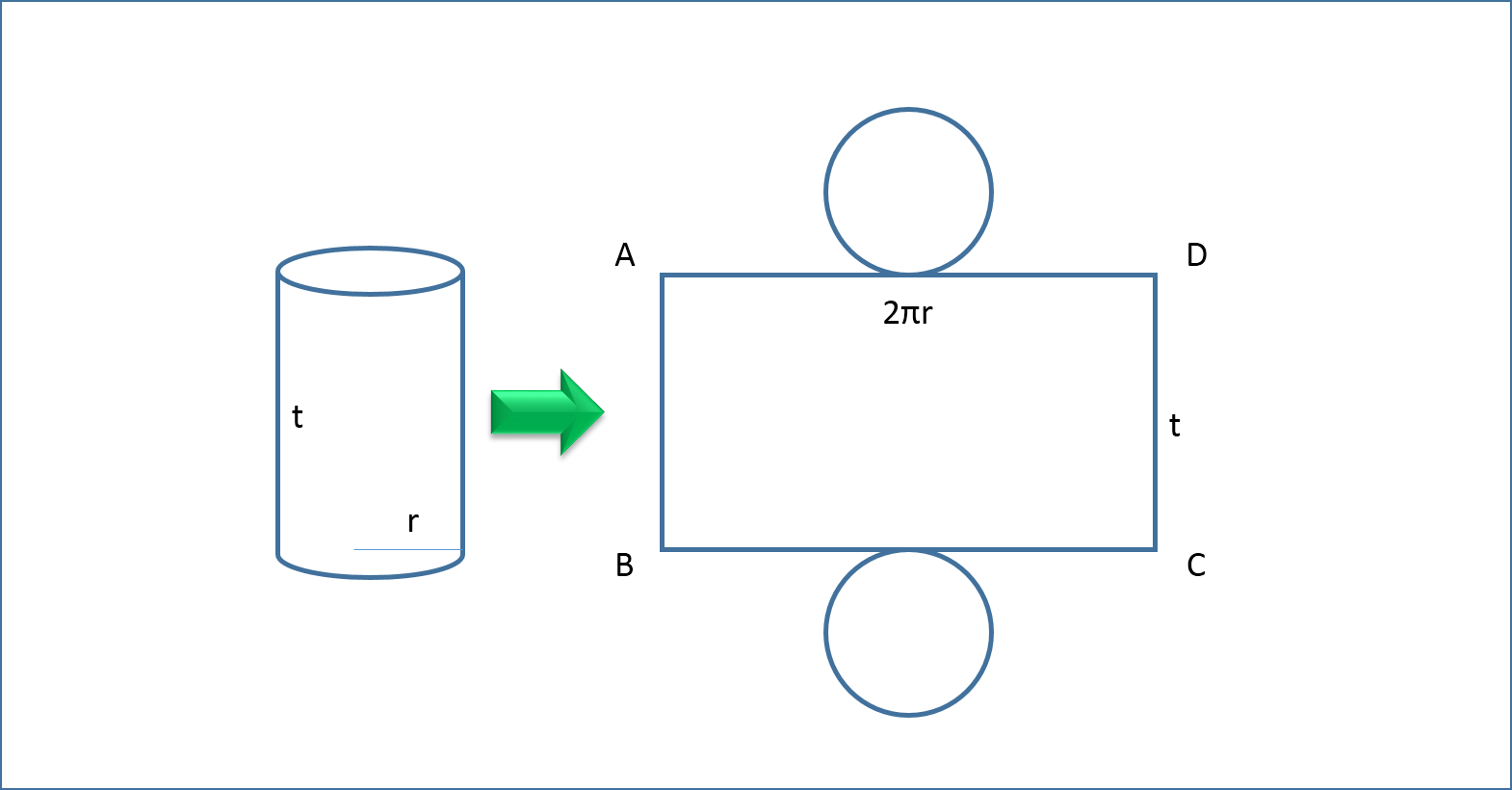
Cara yang baik buat mencari luas suatu bangun ruang adalah dengan membelah bangun tersebut. Kemudian dipecah-pecah serta dicari satu-satu. Dengan ini, kita akan sebagai lebih mudah mengerti dalam mencari rumus luasnya. Contoh soal Mari perhatikan contoh soal dibawah ini.. Contoh soal 1. Sebuah tabung memiliki jari-jari alas 7 centimeter dan tinggi 10 centimeter. Berapakah luas seluruh permukaan tabung tadi? Nah, perhatikan langkah demi langkah dalam merampungkan soal ini.. Langkah 1 => analisa soal Tabung bila dibelah, maka akan membuat misalnya gambar diatas. Tabung terdiri menurut : 2 butir bulat, alas serta tutup Selimut dengan panjang "2πr" dan berbentuk persegi panjang, lebarnya adalah tinggi tabung (t). Jadi buat mencari luas total tabung, tinggal jumlahkan saja ke-tiga bangun tersebut dan ketemulah luasnya. Untuk luas selimut bagaimana? Selimut tabung berbentuk persegi panjang : panjangnya sendiri sama menggunakan keliling lingkaran (2πr ). Lebarnya sama dengan ti...