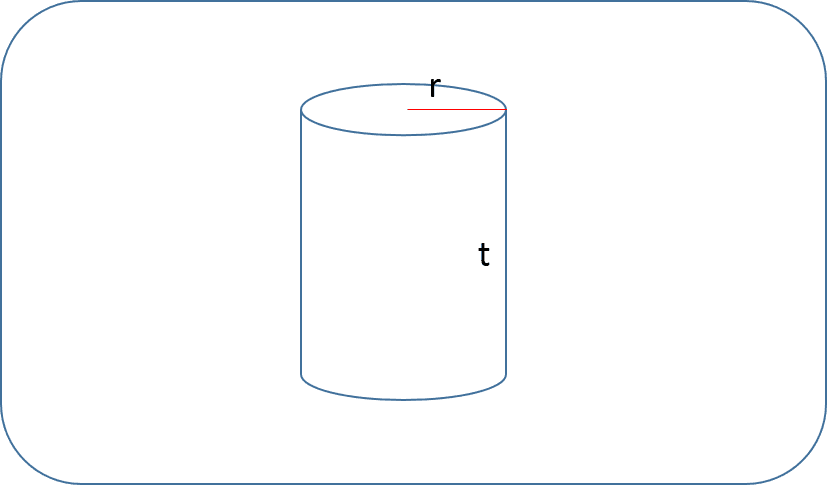
Volume Tabung 10 cmsup3/sup Jika Jarijarinya Tetap dan Tingginya Dinaikkan Dua Kali Semula Berapa Volume Tabung yang Baru Terbaru

Pada awalnya volume tabung telah diketahui, lalu tingginya dinaikkan menjadi dua kali menurut tinggi sebelumnya. Volume yang baru akan dicari. Bisa saja kita mencari tinggi awal dari tabung dulu lalu barulah dijadikan dua kali menurut semula, akan tetapi cara ini agak ribet. Atau sanggup dibilang rumit.. Mengingat nanti yang ketemu adalah tinggi yg mengandung variabel "r" atau jari-jari. Terkesan kurang sederhana.. Nanti kita akan memakai cara perbandingan, sebagai akibatnya prosesnya bisa dipermudah serta volumenya pribadi ditemukan. Soal : 1. Volume suatu tabung adalah 10 cm³. Apabila jari-jarinya permanen dan tingginya dinaikkan menjadi dua kali semula, berapakah volume tabung kini ? Ok, sebelumnya kita korek data-data yg sudah diberikan pada soal. Tabung mula-mula : Volume (V₁) = 10 cm³ jari-jari = r tinggi = t₁ = t Tabung setelahnya : Volume = V₂ (belum diketahui) jari-jari = jari-jari tabung pertama = r (jari-jarinya tetap, lihat dalam soal) tinggi = dua kali menurut t...