Panduan Materi Belajar

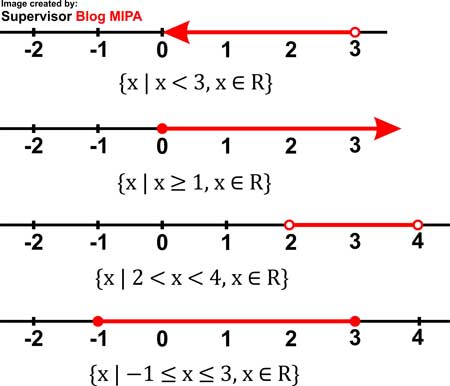
Pengertian selang atau interval dan penyelesaian pertidaksamaan linear merupakan materi prasyarat yang diharapkan untuk memahami materi bahasan penyelesaian pertidaksamaan. Nah, dalam kesempatan kali ini kita akan belajar tentang cara gampang melukiskan grafiks selang dalam pertidaksamaan matematika, baik pertidaksamaan linear maupun kuadrat, keduanya sama saja. Tetapi sebelum itu, kita bahasa dahulu definisi berdasarkan selang. Pengertian Selang Misalkan R adalah himpunan bilangan real. Dari himpunan sapta real R itu, bisa ditentukan himpunan-himpunan bagian R sesuai menggunakan kebutuhan. Sebagai model: ■x x < tiga, x ∈ R ■x x ≥ 1, x ∈ R ■x 2 < x < 4, x ∈ R ■x  −1 ≤ x ≤ 3, x ∈ R Himpunan-himpunan bagian berdasarkan himpunan sapta real R seperti pada contoh di atas dinamakan selang atau interval. Cara Menggambar Selang Suatu Pertidaksamaan Suatu selang bisa digambar dalam garis sapta real berbentuk ruas garis atau segmen garis. Bagian garis yang menyatakan selang tersebut di

Coba kalian perhatikan beberapa bentuk pertidaksamaan berikut ini. ■x2– 4x + 3 < 0 ■x2 + 2x – lima ≤ 0 ■2x2– 11x + 5 > 0 ■3x2– x – dua ≥ 0 Keempat bentuk pertidaksamaan pada atas memuat variabel x berpangkat 2. Pertidaksamaan yg bentuknya demikian diklaim menggunakan pertidaksamaan kuadrat dalam variabel x. Dalam matematika, bentuk baku pertidaksamaan kuadrat pada variabel x terdapat empat macam, yaitu ■ax2 + bx + c < 0 (kurang dari) ■ax2 + bx + c ≤ 0 (kurang dari sama menggunakan) ■ax2 + bx + c > 0 (lebih dari) ■ax2 + bx + c ≥ 0 (lebih dari sama dengan) Dengan a, b serta c merupakan bilangan real serta a ≠ 0. Penyelesaian atau himpunan penyelesaian dari pertidaksamaan kuadrat dalam variabel x bisa ditentukan dengan 2 cara, yaitu menggunakan menggunakan metode berikut adalah. 1. Sketsa grafik fungsi kuadrat 2. Garis bilangan Nah pada kesempatan kali ini, kita akan belajar tentang cara memilih himpunan penyelesaian pertidaksamaan kuadrat dengan menggunakan sketsa grafik fun

Dalam artikel sebelumnya, telah dijelaskan mengenai cara menentukan himpunan penyelesaian pertidaksamaan kuadrat dengan memakai grafik fungsi kuadrat atau grafik parabola. Nah, dalam artikel ini kita akan belajar tentang bagaimana caranya menentukan penyelesaian pertidaksamaan kuadrat dengan menggunakan diagram garis sapta. Sebagai contoh, kita akan memilih himpunan penyelesaian pertidaksamaan kuadrat x2– 4x + 3 < 0 menggunakan memakai metode garis sapta. Langkah-langkah yg perlu kalian lakukan adalah menjadi berikut. Langkah #1 Tentukanlah nilai-nilai nol (bila ada) dari bagian ruas kiri pertidaksamaan kuadrat. Caranya merupakan menggunakan menggunakan metode pemfaktoran yaitu sebagai berikut. ⇔ x2– 4x + 3 = 0 ⇔ (x – 1)(x – 3) = 0 ⇔ x = 1 atau x = 3 Langkah #2 Gambarlah nilai-nilai nol yg diperoleh pada langkah #1 dalam bentuk diagram garis sapta. Dan perlu kalian perhatikan, bahwa nilai-nilai nol tadi membagi garis menjadi 3 interval (selang), yaitu x < 1, 1 < x < tiga