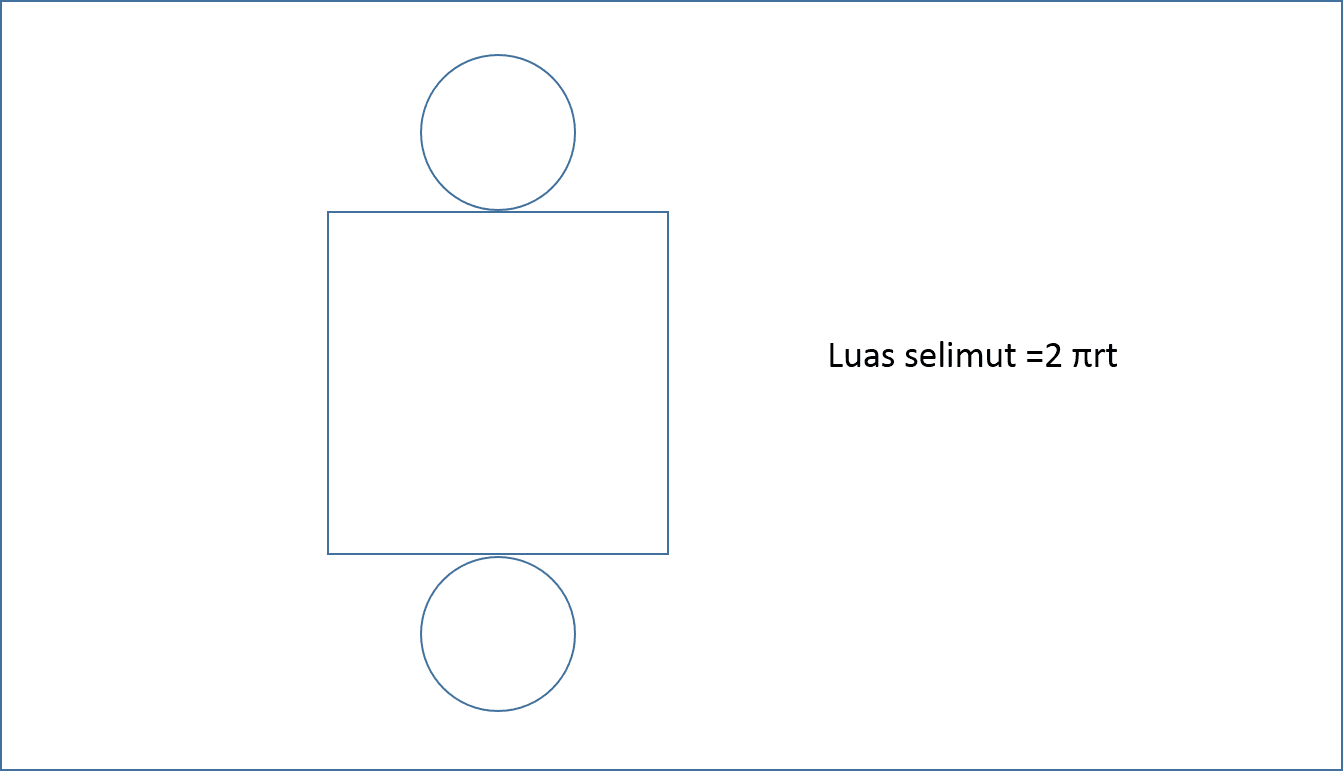
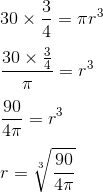Luas Selimut Tabung yang Tingginya 10 cm adalah 440 cmsup2/sup Berapakah Volumenya Terbaru
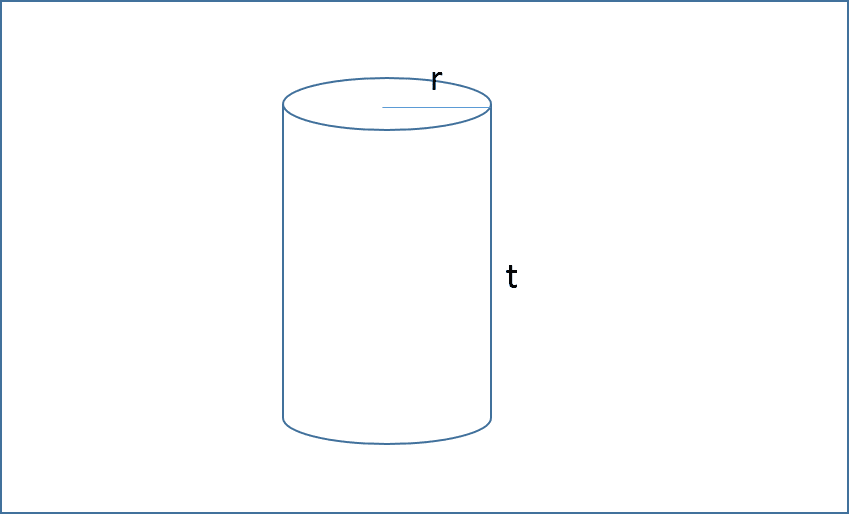
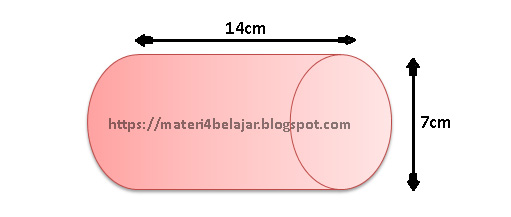
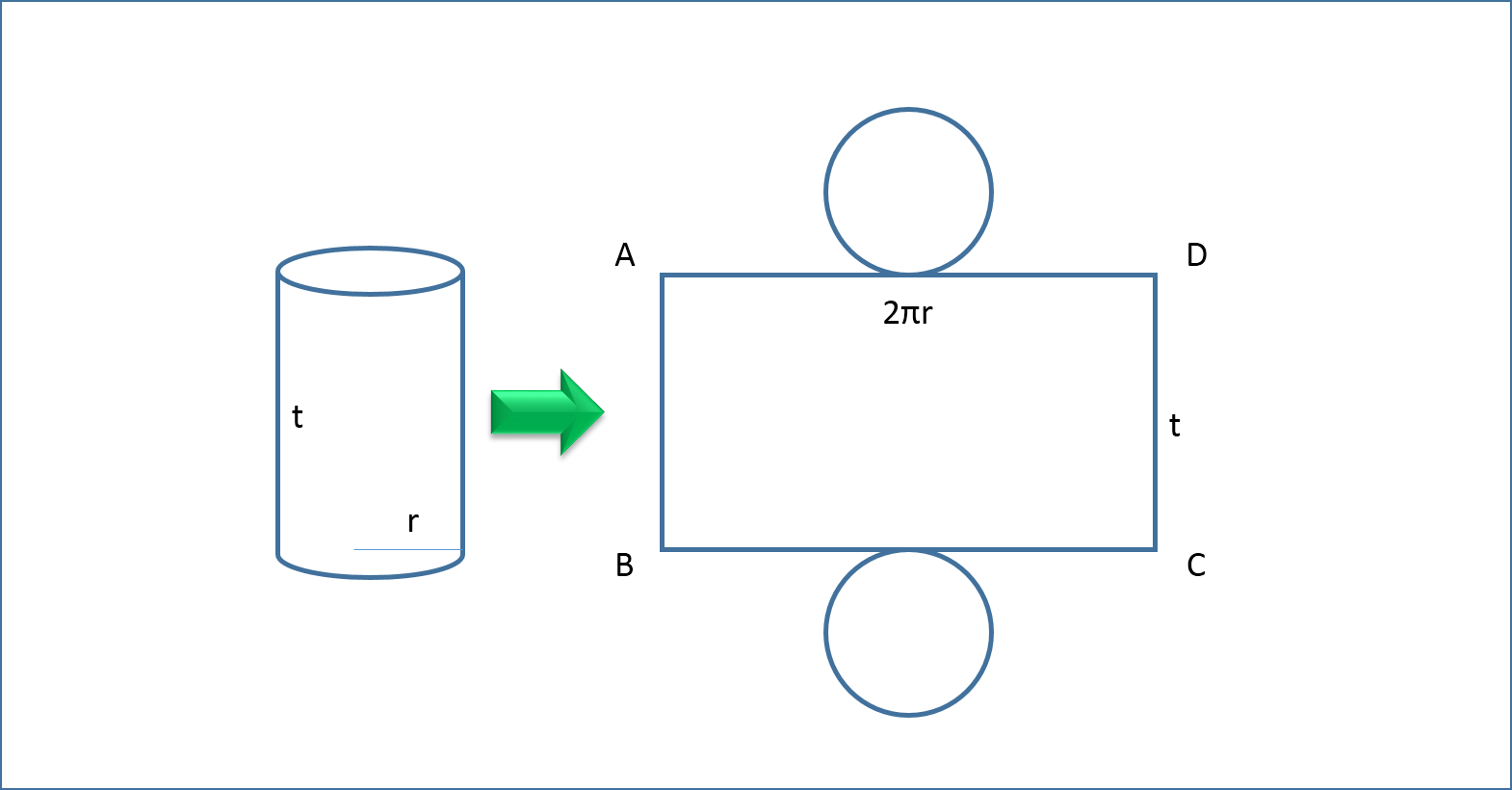
Karena yang diketahui luas selimut, maka kita wajib mengetahui rumus buat luas selimut suatu tabung. Sudah hafal belum? Ok, pada soal berikut akan diberikan rumus selimut tabung dan apa saja yg wajib dicari agar sanggup ditemukan volume tabungnya. Contoh soal : 1. Suatu tabung memiliki luas selimut 440 cm² dan tingginya 10 centimeter. Berapakah volume berdasarkan tabung ini? (π = ²²/₇) Mari lihat gambar tabung dibawah ini.. Dalam soal diatas, jari-jari (r) tabung belum diketahui dan inilah yang harus kita cari menggunakan bantuan berdasarkan luas selimut. Mencari jari-jari (r) Ok, rumus berdasarkan luas selimut tabung adalah.. Luas selimut = 2πr × t Diketahui : luas selimut = 440 cm² tinggi (t) = 10 cm π = ²²/₇ Masukkan yang diketahui ke pada rumus luas selimut.. 440 = 2 × ²²/₇ × r × 10 440 = ⁴⁴⁰/₇ × r Untuk menerima "r", maka bagi 440 dengan ⁴⁴⁰/₇ r = 440 : ⁴⁴⁰/₇ r = 440 × ⁷/₄₄₀ Jika dibagi menggunakan pecahan, maka tanda bagi berubah sebagai kali serta pecahan yg dibelakan...