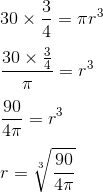Panduan Materi Belajar

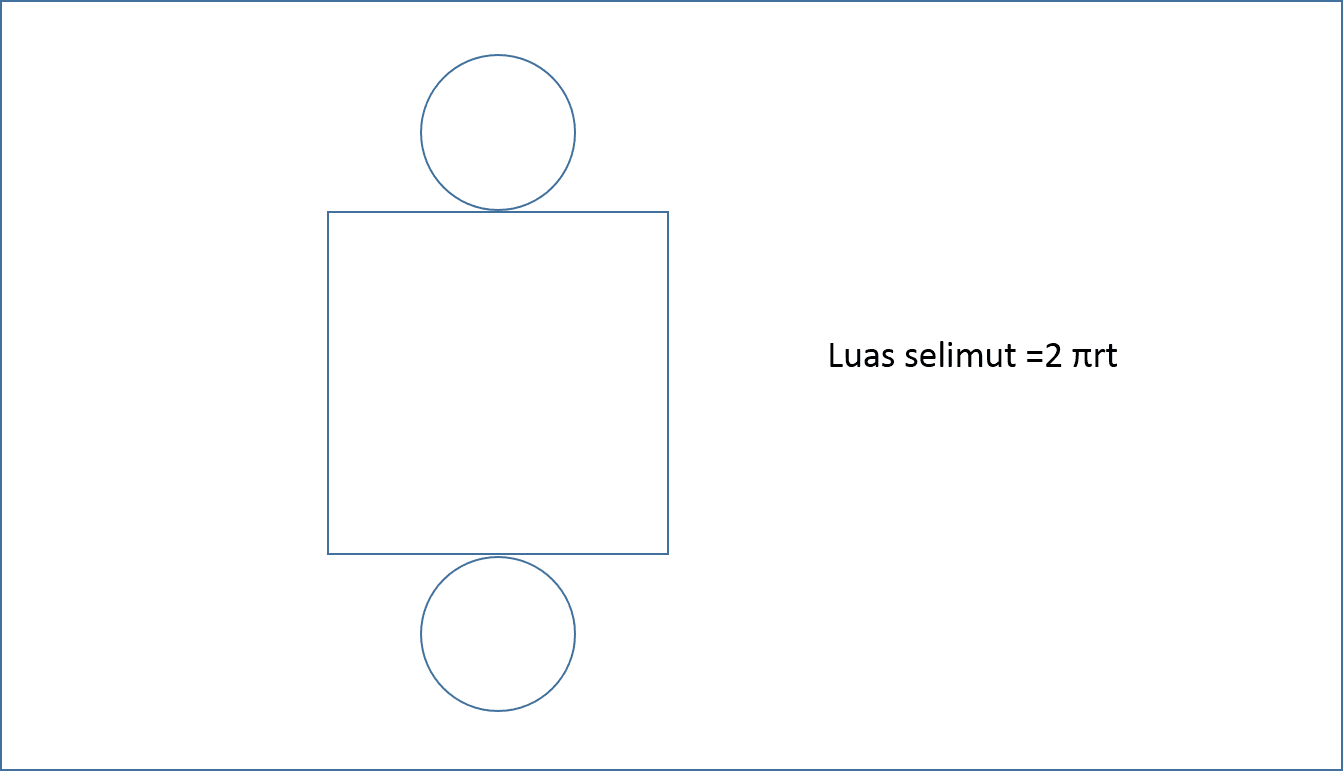
Masih jangan lupa dengan volume tabung? Baik jikalau masih jangan lupa, tidak terdapat salahnya aku ingatkan lagi ya!! Rumus volume tabung = πr²×t. Nah, dalam soal diatas diketahui luas alasnya dan alas berdasarkan tabung berbentuk lingkaran. Berarti kita harus mencari jari-jarinya dulu ya? Boleh.. Tapi itu kelamaan.. Karena kita melakukan perhitungan sebesar 2 kali serta ini pastinya membuang waktu. Untuk itu saya akan menyebutkan bagaimana mencari luas menurut sebuah tabung apabila diketahui luas alas dan tingginya. Contoh soal : 1. Sebuah tabung memiliki luas alas 30 cm² dan tingginya lima cm. Berapakah volume menurut tabung tersebut? Diatas sudah aku jelaskan jikalau anda ingin mencari jari-jarinya (r) lebih dulu, boleh kok. Tapi itu pemborosan saat. Mengapa? Mari perhatikan luas alas serta rumus tabungnya. Alas tabung berbentuk bulat, dan luasnya merupakan πr². Sekarang perhatikan rumus volume tabung : Volume = ( πr² )×t Coba perhatikan yang terdapat pada kurung dalam rumus diata

Tabung merupakan bangun ruang yang alas dan tutupnya berbentuk lingkaran. Untuk menerima luas dan volumenya, kita mampu menggunakan rumus yg sudah terdapat. Mari kerjakan soalnya.. Soal : 1. Sebuah tabung memiliki jari-jari 7 centimeter dan tingginya 8 cm. Berapakah volume dan luas tabung tersebut?? Dalam soal sudah diketahui beberapa data : Jari-jari (r) = 7 cm tinggi (t) = 8 cm Kita cari satu per satu. Luas tabung Rumus untuk luas tabung adalah : Luas = 2 × luas alas + luas selimut tabung Luas = 2πr² + 2πrt Atau.. Luas = 2πr (r+t) Masukkan : r = 7 cm t = 8 cm π = ²²/₇ (karena jari-jari kelipatan berdasarkan 7) Luas = 2πr (r+t) Luas = 2 × ²²/₇ × 7 × (7+8) Luas = dua × 22 × (15) Luas = 660 cm² Volume Untuk volume tabung, rumusnya seperti dibawah : Volume = Luas alas × tinggi karena alasnya bundar, maka luas alas adalah luas lingkaran Volume = πr²× t Masukkan data yang diketahui  r = 7 cmt = 8 cmπ = ²²/₇  Volume = πr²× t Volume = ²²/₇ × 7² × 8 Volume = 154 × 8 Volume = 1.232 cm³ Soal :

Ok.. Sekarang kita akan mencari bagaimana cara mendapatkan luas bagian atas dari sebuah tabung yang diketahui volume serta tingginya. Karena nanti dalam soal diketahui volumenya, maka kita akan menggunakan donasi dari volume buat menerima data mengenai tabung yg belum diketahui. Biar lebih jelas, kita eksklusif kerjakan soalnya.. Soal : 1. Sebuah tabung diketahui volumenya 1570 cm³ dan tingginya lima cm. Berapakah luas permukaannya? (π = tiga,14) Pada tabung diatas, kita belum mengetahui jari-jarinya. Dan langkah pertama yang harus dilakukan adalah mencari berapa panjangnya. Mencari jari-jari (r) Kita akan menggunakan rumus volume buat membantu menemukan jari-jari menurut tabung ini. Volume tabung = πr²×t volume = 1570 t = lima cm π =  tiga,14 1570 = 3,14 × r² × 5 1570 = 15,7 × r² untuk menerima r², maka 1570 dibagi dengan 15,7 r² = 1570 : 15,7 r² = 100 untuk menerima r, akarkan 100 r = √100 r = 10 cm. Mencari luas bagian atas tabung Jari-jari telah diperoleh serta sekarang saatnya bu

Karena diketahui luas selimut, maka data ini akan dipakai buat menemukan unsur yg belum diketahui. Masih jangan lupa menggunakan rumus selimut tabung? Mari kita kerjakan soalnya.. Contoh soal : 1. Sebuah tabung mempunyai luas selimut 880 cm² serta tingginya 10 cm. Berapakah volumenya? (π = ²²/₇) Diketahui dalam soal luas selimut = 880 cm² dan tinggi 10 cm. Kita gunakan rumus luas selimut buat mendapatkan jari-jari tabung, sebagai akibatnya volumenya sanggup dihitung. Luas selimut = 2πrt ganti luas selimut menggunakan 880 ganti tinggi dengan 10 880 = dua ײ²/₇ × r × 10 880 = ⁴⁴⁰/₇ × r untuk mendapatkan r, bagi 880 menggunakan 440 per 7 r = 880 : ⁴⁴⁰/₇ ubah tanda bagi sebagai kali dan 7 diatas sedangkan 440 dibawah. r = 880 × ⁷/₄₄₀ bagi 880 dengan 440 hasilnya2, kemudian kalikan menggunakan 7 serta hasilnya 14 r = 14 cm. Jari-jari sudah diperoleh, kini kita sanggup mencari volume dari tabung.. Volume tabung Volume tabung = πr² × t Volume tabung = ²²/₇ × 14² × 10 Volume tabung = 6160 cm³

Pada awalnya volume tabung telah diketahui, lalu tingginya dinaikkan menjadi dua kali menurut tinggi sebelumnya. Volume yang baru akan dicari. Bisa saja kita mencari tinggi awal dari tabung dulu lalu barulah dijadikan dua kali menurut semula, akan tetapi cara ini agak ribet. Atau sanggup dibilang rumit.. Mengingat nanti yang ketemu adalah tinggi yg mengandung variabel "r" atau jari-jari. Terkesan kurang sederhana.. Nanti kita akan memakai cara perbandingan, sebagai akibatnya prosesnya bisa dipermudah serta volumenya pribadi ditemukan. Soal : 1. Volume suatu tabung adalah 10 cm³. Apabila jari-jarinya permanen dan tingginya dinaikkan menjadi dua kali semula, berapakah volume tabung kini ? Ok, sebelumnya kita korek data-data yg sudah diberikan pada soal. Tabung mula-mula : Volume (V₁) = 10 cm³ jari-jari = r tinggi = t₁ = t Tabung setelahnya : Volume = V₂ (belum diketahui) jari-jari = jari-jari tabung pertama = r (jari-jarinya tetap, lihat dalam soal) tinggi = dua kali menurut t

Mari kita eksklusif kerjakan soalnya.. Soal : 1. Sebuah bola mempunyai volume 30 cm². Jika jari-jari bola ini dijadikan dua kali semula, berapakah volumenya kini ? Kita bagi syarat bola menjadi 2, yaitu bola pertama dan bola ke 2. Kondisi bola pertama merupakan : volume = 30 cm² jari-jari = r Sekarang kita masuk ke bola kedua, kondisinya merupakan : volume =...? jari-jari = 2 kali jari-jari pertama = 2r. Ini mampu diselesaikan dengan 2 cara dan keduanya akan dibahas menjadi perbandingan, apakah hasilnya sama atau tidak. Cara pertama Kita akan mencari berapa jari-jari dari syarat pertama.. volume bola = ⁴/₃πr³ ganti volume bola dengan 30 30 = ⁴/₃πr³ empat per 3 dipindah ke ruas kiri sebagai akibatnya menjadi kali serta posisinya berubah sebagai tiga per 4 30 × ³/₄ = πr³ phi dipindahkan ke ruas kiri sebagai akibatnya sebagai pembagi. Sekarang r sudah diperoleh serta kita sanggup mencari jari-jari bola ke 2. Jari-jari bola ke 2 adalah dua kali jari-jari pertama =2r. Jari-jari bola ke 2 m

Bentuk dari kerucut yang terpotong, sangat mirip menggunakan ember yg sehari-hari kita gunakan. Nah inilah yg akan dicari volumenya. Soal : 1. Sebuah benda (kerucut terpotong), mempunyai jari-jari mini dan jari-jari akbar masing-masing tiga centimeter serta 6 cm. Tingginya 4 cm. Berapakah volume menurut benda tersebut?  Gambar dari benda tersebut bisa dilihat dibawah ini.. Untuk menerima volumenya, kita wajib membaginya menjadi dua buah kerucut, yaitu kerucut akbar dan kerucut kecil. Gambar orisinil kita panjangkan ke atas, sehingga sebagai kerucut yang lebih kecil. Kerucut kecil = ABC Kerucut besar = ADE Volumenya dicari dengan cara mengurangkan kerucut besar dengan kerucut mini , maka isi bendanya bisa ditemukan. Tapi terdapat masalah.. Kita belum memahami berapa tinggi kerucut kecil kan? Tinggi kerucut kecil Saya akan menaruh rumus singkat untuk menerima tinggi kerucut kecil. Rumusnya merupakan : t = tinggi kerucut kecil n = tinggi benda r 1 = jari-jari kerucut kecil r 2 = jari-j