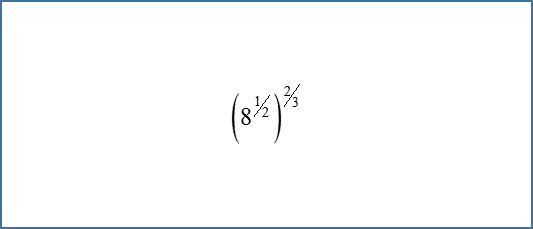Panduan Materi Belajar

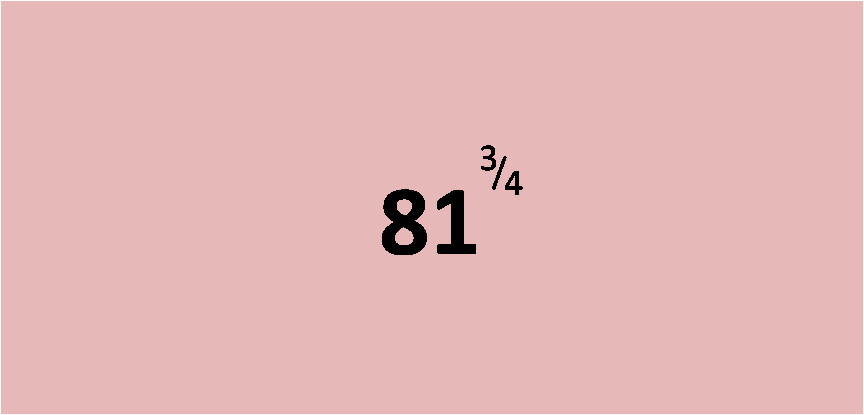
Ok, kita akan mengerjakan soal tentang perpangkatan. Untuk lebih jelasnya, perhatikan contoh soalnya dibawah ini.. Soal : 1. Berapakah hasil menurut 813/4  ? Mari kita kerjakan.. 81 bisa diubah sebagai tiga pangkat 4, jadi.. (81)3/4  = (3⁴)3/4 kalau pangkat pada pangkatkan lagi, itu merupakan pangkatnya dikali. = (3) 4 × tiga/4 = (tiga) 12/4 = (tiga)3 = 3 × tiga × 3 = 27. Jadi, output berdasarkan (81)3/4  = 27 Soal : 2. Berapakah output menurut 3125 2/5  ? Masih sama menggunakan soal diatas.. 3125 sanggup diubah sebagai 5 pangkat lima, jadi.. (3125)2/5  =  (5⁵)2/5 kalau pangkat pada pangkatkan lagi, itu merupakan pangkatnya dikali. = (lima) lima × 2/5 = (5) 10/5 = (5)2 = lima × 5 = 25. Jadi, output dari (3125)dua/5  = 25 Soal : 3. Berapakah output berdasarkan 16 5/4  ? 16 mampu diubah sebagai 2 pangkat 4, jadi.. (16)5/4  =  (2⁴)5/4 kalau pangkat pada pangkatkan lagi, itu merupakan pangkatnya dikali. = (dua) 4 × 5/4 = (2) 20/4 = (dua)5 = dua × dua × 2 × 2 × 2 = 32. Jadi, output berdasa

  Ini merupakan soal dalam bentuk eksponen dan terdapat beberapa sifat yg akan membantu kita dalam menyelesaikan persoalan misalnya ini. Ok, kita ulang dulu soalnya ayo.. Contoh soal : 1. Berapakah nilai menurut [81/2]dua/3?  Mari kita hukuman.. Langkah 1 → Analisa soal Mari lihat sifat perpangkatan dibawah ini.. ⇥ [ab]c = abxc   ...............(1) ⇥ ab x ac = ab+c...............(dua) Coba perhatikan, sifat manakah yang akan kita gunakan? Tentu saja yg ke 2 nir bisa diterapkan. Karena soal kita merupakan pangkat yg dipangkatkan lagi.. Jadi yang dipakai merupakan sifat yg pertama.. Langkah dua → Mengerjakan soal Sekarang yuk kita kerjakan soalnya.. Sifat yang digunakan merupakan sifat pertama.. = [81/2]dua/3 = [8]1/dua  x  2/3 = 81/3 = [23]1/3 = [2] 3 x1/3 = 21 = 2 ♣ Pangkat 8 yang 1 / 2 dikalikan menggunakan 2 / 3 ♣ Hasilnya adalah 1 / 3 ♣ 8 diubah menjadi 23 dan pangkat 1 / 3 masih permanen. ♣ Kalikan lagi 3 menggunakan 1 / 3 serta hasilnya adalah 1. ♣ Jadi jawabannya adalah 2. Mudah

Kebingungan mencari KPK serta FPB dari soal dengan contoh misalnya ini? Nah, disini akan dijelaskan bagaimana langkah mudah dalam menemukan jawaban berdasarkan soal homogen. Praktis kok.. Nanti akan dijelaskan lebih rinci bagaimana caranya.. Sekarang kita pribadi lihat saja soalnya.. Soal : 1. Berapakah KPK dan FPB menurut 4a²b³ serta 6a³b²? Ok.. Kita cari satu-satu.. Mencari KPK KPK merupakan Kelipatan Persekutuan Terkecil menurut suatu sapta atau angka yang diberikan. Kita akan mencari satu-satu kelipatannya. Biar lebih jelas perhatikan lagi ya!! 4a²b³ serta 6a³b² Angka dulu Kita cari yang nomor dulu. Diketahui terdapat nomor 4 serta 6. Sudah memahami KPK dari 4 dan 6? Jawabannya adalah 12. Jadi KPK pertama kita adalah 12. Ini disimpan dulu, nanti akan dipakai lagi. Huruf "a" Dalam soal terdapat huruf "a". Diketahui : Pada 4a²b³, huruf "a"-nya merupakan a² Pada 6a³b², huruf "a"-nya merupakan a³ Kita akan mencari KPK dari a² dan a³.  Trik gampa

Dalam artikel tentang bentuk pangkat sapta bulat , sudah dijelaskan bahwa pengertian sapta berpangkat adalah bentuk perkalian sapta-bilangan yg sama atau perkalian berulang yang dibagi sebagai 2 macam yaitu pangkat bulat positif serta pangkat bulat negatif. Notasi sapta berpangkat adalahanyang berarti perkalian bilanganasecara berulang sebanyakn. Misalkan 72= 7 x 7. Nah kini yang sebagai pertanyaannya merupakan bagaimana dengan bentuk 71/dua? Apa merupakan dan Bagaimana cara solusinya? Bentuk 71/2adalah bentukbilangan berpangkat pecahan.lalu apa itu bilangan berpangkat pecahan? Untuk menjawab pertanyaan tersebut silahkan simak penjelasan mengenai pengertian, rumus, model soal serta pembahasan tentang bilangan pangkat pecahan ini dia. Pengertian Bilangan Berpangkat Pecahan Pangkat pecahan ini herbi operasi bentuk akar . Kita memahami bahwa pecahan adalah suatu bentuk bilangan yang dituliskan sebagaim/ndenganm, n∈bilangan bulat dan n≠0.dan bentuk bilangan berpangkat pecahan secara gener

Ini merupakan model soal eksponen namun nomor yg dipakai tidak sama. Apa yang akan kita lakukan apabila menemukan soal contoh diatas? Apakah memangkatkan satu demi satu? Boleh kok.. Tapi tentu lebih ribet serta membuat perhitungan memakan waktu yang lebih usang dan kemungkinan galat semakin akbar.. Mau? Dibawah ini akan dijelaskan bagaimana cara menyiasati soal seperti itu agar lebih gampang dikerjakan serta menghilangkan kesan ribet.. Soal : 1. Berapakah nilai dari 6³ × 5⁴  : 15²? Model soal seperti ini sanggup kita ubah bentuknya menjadi dibawah.. Sekarang dipecah lagi dengan membarui pangkat menjadi perkalian.. Disini kita hilangkan bentuk pangkatnya dulu.. Kita sederhanakan dulu dengan membagi lima dengan 15 Ada 2 yg sanggup disederhanakan, mengingat hanya ada dua angka 15 dibawahnya. 5 serta 15 sama-sama dibagi lima, sebagai akibatnya hasilnya seperti diatas.. 5 dibagi lima = 1 15 dibagi lima = 3 Sekarang, sederhanakan 6 menggunakan 3. 6 dibagi tiga = 2 3 dibagi 3 = 1 Hasilnya su

Bilangan dengan pangkat desimal, sanggup dilakukan pengubahan sedikit sehingga bentuknya lebih mudah dipahami. Pangkatnya mampu dijadikan pecahan dulu. Mari kita coba soalnya.. Soal : 1. Berapakah nilai berdasarkan 320,dua ? Kita ubah dulu pangkatnya yang 0,dua menjadi pecahan. 0,2 = ²∕₁₀ sederhanakan dengan membagi pembilang dan penyebut menggunakan 2 = ¹∕₅ Sehingga 0,2 = ¹∕₅ Kemudian masuk ke soal primer.. = (32)0,2 = (32) 1/5 Ubah 32 sebagai bentuk pangkat 32 = 2⁵ = (2⁵) 1/5 Gunakan sifat berikut : (ab)c = (a)b×c Sehingga : = (2⁵) 1/5 = (2)lima×1/lima  5× ⅕ = 1 = (2)¹ = 2 Sehingga diperoleh jikalau (32)0,dua =  2 Soal : 2. Berapakah nilai dari 161,25 ? Sekarang, kita nir mengganti pangkatnya sebagai pecahan, abaikan saja pada bentuk desimal. Hasilnya sama saja bila memakai pecahan. Soalnya adalah : = (16)1,25 Ubah 16 sebagai bentuk pangkat 16 = 2⁴ = (2⁴)1,25 Gunakan sifat berikut : (ab)c = (a)b×c Sehingga : = (2⁴)1,25 = (dua)4×1,25  4 × 1,25 = 5 = (2)⁵ = 32 Sehingga diperoleh kalau

Kali ini kita akan menyederhanakan bentuk perpangkatan serta memakai sifat-sifat generik yg berlaku. Mari kita coba.. Soal : Caranya misalnya ini : Langkahnya : Kumpulkan bilangan pangkat yang sama, a dengan a, dan b menggunakan b Ketika dua sapta pangkat dibagi, maka pangkatnya dikurang. b pangkat -1 diubah menjadi b pangkat 1 dengan menukar posisinya ke bawah. Soal : Jawabannya : Langkahnya : Karena dibagi, kurangkan pangkat berdasarkan a, b atau c a pangkat -4 dibentuk positif menggunakan cara membawanya ke bawah menjadi penyebut pecahan Soal : Langkahnya misalnya ini : Panduan : Ketika ada pangkat yg dipangkatkan lagi, maka pangkatnya dikali Soal : Caranya : Panduan : Semua bilangan yg terdapat didalam kurung dikalikan pangkatnya menggunakan 3 Atau output diatas pula bisa ditulis menjadi = (ab)⁴ Silahkan baca pula : #8 Cara Menyederhanakan Soal Perpangkatan Hasil Dari 81 Pangkat tiga/4 #4 Cara Lain Mencari 4 pangkat 3/dua serta 8 pangkat dua/3

Dalam artikel tentang definisi serta notasi logaritma , sudah dijelaskan bahwa logaritma merupakan invers atau kebalikan dari pemangkatan . Ketika kita mencari nilai logaritma suatu sapta berarti kita sedang mencari pangkat berdasarkan suatu sapta pokok sebagai akibatnya hasilnya sesuai menggunakan yang telah diketahui. Untuk mencari logaritma suatu sapta, kita bisa memakai tabel logaritma biasa . Namun pada matematika, nilai logaritma suatu bilangan nir harus dicari menggunakan menggunakan tabel logaritma, karena logarima mempunyai beberapa sifat atau rumus identitas yang bisa dipergunakan buat menentukan nilai logaritma suatu bilangan menggunakan kondisi atau syarat eksklusif. Ini dia merupakan gambar sifat-sifat logaritma yang telah penulis rangkum. Untuk memahami sifat-sifat logaritma, cara verifikasi sifat atau rumus logaritma dan contoh soal yang berkaitan dengan sifat-sifat operasi hitung logaritma, silahkan kalian pelajari uraian artikel berikut ini. Bentuk Umum Logaritma ax=