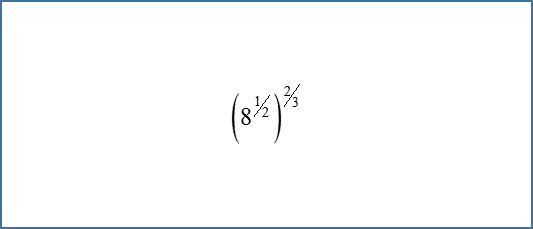Panduan Materi Belajar

Bilangan dengan pangkat desimal, sanggup dilakukan pengubahan sedikit sehingga bentuknya lebih mudah dipahami. Pangkatnya mampu dijadikan pecahan dulu. Mari kita coba soalnya.. Soal : 1. Berapakah nilai berdasarkan 320,dua ? Kita ubah dulu pangkatnya yang 0,dua menjadi pecahan. 0,2 = ²∕₁₀ sederhanakan dengan membagi pembilang dan penyebut menggunakan 2 = ¹∕₅ Sehingga 0,2 = ¹∕₅ Kemudian masuk ke soal primer.. = (32)0,2 = (32) 1/5 Ubah 32 sebagai bentuk pangkat 32 = 2⁵ = (2⁵) 1/5 Gunakan sifat berikut : (ab)c = (a)b×c Sehingga : = (2⁵) 1/5 = (2)lima×1/lima  5× ⅕ = 1 = (2)¹ = 2 Sehingga diperoleh jikalau (32)0,dua =  2 Soal : 2. Berapakah nilai dari 161,25 ? Sekarang, kita nir mengganti pangkatnya sebagai pecahan, abaikan saja pada bentuk desimal. Hasilnya sama saja bila memakai pecahan. Soalnya adalah : = (16)1,25 Ubah 16 sebagai bentuk pangkat 16 = 2⁴ = (2⁴)1,25 Gunakan sifat berikut : (ab)c = (a)b×c Sehingga : = (2⁴)1,25 = (dua)4×1,25  4 × 1,25 = 5 = (2)⁵ = 32 Sehingga diperoleh kalau

Untuk sanggup mendapatkan bentuk sederhana berdasarkan suatu pembagian, kita bisa memfaktorkannya lebih dulu.. Kemudian barulah sanggup dibagi.. Ok.. Tidak perlu menunggu usang lagi.. Langsung saja kita coba beberapa contoh soal menyederhanakan pembagian yg terdiri menurut beberapa variabel.. 1. Bentuk sederhana dari pecahan berikut merupakan :  Langkah pertama yg harus dilakukan merupakan memfaktorkan bentuknya dan yang sanggup difaktorkan merupakan bentuk dalam pembilang (permukaan), yaitu "ap + a". Perhatikan!! ap + a sama-sama mengandung "a" Langkahnya : "a" ditarik keluar dan berada diluar kurung. karena "a" ditarik keluar, maka "a" sekarang menjadi pembagi yang ada didalam. "ap" dibagi dengan "a" sisanya p "a" dibagi dengan "a" sisanya 1 Sehingga "ap+a" = a(p+1) Kemudian : bagi "a" diatas dan yg dibawah. sehingga hasilnya merupakan "p+1" 2. Bentuk sederhana dar

  Ini merupakan soal dalam bentuk eksponen dan terdapat beberapa sifat yg akan membantu kita dalam menyelesaikan persoalan misalnya ini. Ok, kita ulang dulu soalnya ayo.. Contoh soal : 1. Berapakah nilai menurut [81/2]dua/3?  Mari kita hukuman.. Langkah 1 → Analisa soal Mari lihat sifat perpangkatan dibawah ini.. ⇥ [ab]c = abxc   ...............(1) ⇥ ab x ac = ab+c...............(dua) Coba perhatikan, sifat manakah yang akan kita gunakan? Tentu saja yg ke 2 nir bisa diterapkan. Karena soal kita merupakan pangkat yg dipangkatkan lagi.. Jadi yang dipakai merupakan sifat yg pertama.. Langkah dua → Mengerjakan soal Sekarang yuk kita kerjakan soalnya.. Sifat yang digunakan merupakan sifat pertama.. = [81/2]dua/3 = [8]1/dua  x  2/3 = 81/3 = [23]1/3 = [2] 3 x1/3 = 21 = 2 ♣ Pangkat 8 yang 1 / 2 dikalikan menggunakan 2 / 3 ♣ Hasilnya adalah 1 / 3 ♣ 8 diubah menjadi 23 dan pangkat 1 / 3 masih permanen. ♣ Kalikan lagi 3 menggunakan 1 / 3 serta hasilnya adalah 1. ♣ Jadi jawabannya adalah 2. Mudah

Dalam artikel tentang definisi serta notasi logaritma , sudah dijelaskan bahwa logaritma merupakan invers atau kebalikan dari pemangkatan . Ketika kita mencari nilai logaritma suatu sapta berarti kita sedang mencari pangkat berdasarkan suatu sapta pokok sebagai akibatnya hasilnya sesuai menggunakan yang telah diketahui. Untuk mencari logaritma suatu sapta, kita bisa memakai tabel logaritma biasa . Namun pada matematika, nilai logaritma suatu bilangan nir harus dicari menggunakan menggunakan tabel logaritma, karena logarima mempunyai beberapa sifat atau rumus identitas yang bisa dipergunakan buat menentukan nilai logaritma suatu bilangan menggunakan kondisi atau syarat eksklusif. Ini dia merupakan gambar sifat-sifat logaritma yang telah penulis rangkum. Untuk memahami sifat-sifat logaritma, cara verifikasi sifat atau rumus logaritma dan contoh soal yang berkaitan dengan sifat-sifat operasi hitung logaritma, silahkan kalian pelajari uraian artikel berikut ini. Bentuk Umum Logaritma ax=

Dengan menggunakan beberapa sifat perpangkatan, model pembagian misalnya ini bisa dituntaskan menggunakan cepat tanpa perhitungan ribet. Kita coba.. Soal : 1. Sederhanakan bentuk perpangkatan ini, 2⁴ : 4⁴ !! Mari kita tuntaskan!! Bentuk perpangkatan mampu diubah misalnya diatas Karena pangkatnya sama-sama 4, jadi ditulis satu saja Kita bisa menyederhanakan ²∕₄ Hasilnya menjadi ½ Karena bentuknya sudah sederhana, sekarang kita bisa mengembalikan lagi ke bentuk awal Pembilang serta penyebut sama-sama menerima pangkat 4 1⁴ = 1 2⁴ = 16 Sehingga output sederhananya adalah ¹∕₁₆ Soal : 2. Sederhanakan bentuk pangkat → 6³ : 8³ !! Kita coba satu soal lagi.. Pangkatnya sama, yaitu 3, sehingga bisa dimuntahkan dan ditulis satu saja. ⁶∕₈ bisa disederhanakan, sama-sama dibagi 2 hasilnya adalah ³∕₄ Karena sudah sederhana, sekarang kita tempatkan lagi pangkatnya dipembilang serta penyebutnya. 3 mendapatkan pangkat 3, hasilnya 27 4 mendapatkan pangkat 3, hasilnya 64 Sehingga hasil sederhana menurut p

Bentuk Umum Pertidaksamaan Linear Perhatikan beberapa bentuk pertidaksamaan ini dia. (i) 2x – 1 < 0 (ii) 6x + 4 ≤ 0 (iii) 3x – 6 > 0 (iv) 2x – lima ≥ 0 Setiap pertidaksamaan pada atas memuat variabel x berpangkat atau berderajat 1 (satu). Pertidaksamaan yg berciri demikian dinamakan pertidaksamaan linear pada variabel x. Bentuk generik (baku) dari pertidaksamaan linear dalam variabel x ada 4 macam, yaitu menjadi berikut: ■ax + b < 0 ■ax + b ≤ 0 ■ax + b > 0 ■ax + b ≥ 0 Cara Penyelesaian Pertidaksamaan Linear Satu Variabel Menyelesaikan sebuah pertidaksamaan linear satu variabel bisa diartikan menjadi mencari bentuk paling sederhana menurut pertidaksamaan linear tadi. Bentuk paling sederhana ini dianggap penyelesaian dari pertidaksamaan linear satu variabel. Penyelesaian dari suatu pertidaksamaan diperoleh dengan proses manipulasi aljabar terhadap pertidaksamaan semula. Dalam proses manipulasi aljabar buat menentukan penyelesaian suatu pertidaksamaan, digunakan sifat-sifat s