Panduan Materi Belajar

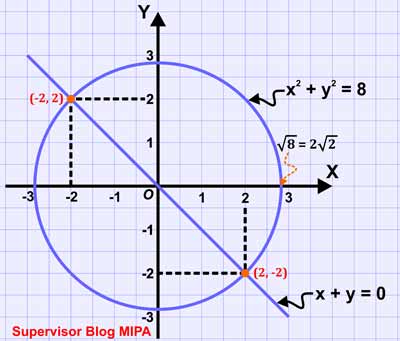
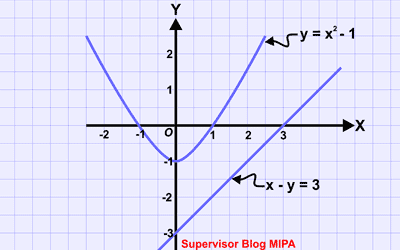
Sistem persamaan linear dan kuadrat atau disingkat SPLK adalah sistem persamaan matematika yg terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yg masing-masing bervariabel 2. Berdasarkan karakteristik dan bagian bentuk kuadratnya, sistem persamaan linear serta kuadrat (SPLK) bisa dibedakan menjadu 2 jenis, yaitu: 1. SPLK menggunakan bagian kuadrat berbentuk eksplisit 2. SPLK menggunakan bagian kuadrat berbentuk implisit Suatu persamaan dua peubah x serta y dikatakan berbentuk eskplisit bila persamaan itu bisa dinyatakan dalam bentuk y = f(x) atau x = f(y). Contoh persamaan dua peubah/variabel (x serta y) pada bentuk eksplisit adalah sebagai berikut. i) y = 3x – 2 ii) x = lima – 4y iii) y = x2– 4x + 5 iv) x = 3y2 + 6y – 2 Persamaan 2 peubah x serta y dikatakan berbentuk implisit bila persamaan itu nir dapat dinyatakan dalam bentuk y = f(x) atau x = f(y). Persamaan implisit dinyatakan dalam bentuk f(x, y) = 0. Contoh persamaan dua peubah (x serta y) dalam bentuk tersir

Sistem persamaan linear serta kuadrat atau disingkat SPLK merupakan sistem persamaan yg terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yang masing-masing bervariabel dua. SPLK dibedakan sebagai 2 jenis dari bentuk kuadratnya, yaitu SPLK dengan bagian kuadrat berbentuk eksplisit dan SPLK dengan bagian bagian kuadrat berbentuk implisit. Secara umum, SPLK menggunakan bagian kuadrat berbentuk implisit bisa dituliskan sebagai berikut. px + qy + r = 0 ……………. (bagian linear) ax2 + by2 + cxy + dx + ey + f = 0 ……………. (bagian kuadrat) Dengan a, b, c, d, e, f, p, q, dan r adalah sapta-sapta real. SPLK menggunakan bagian kuadrat yang berbentuk implisit ada dua kemungkinan, yaitu: 1. SPLK bentuk tersirat yang tak bisa difaktorkan 2. SPLK bentuk implisit yang dapat difaktorkan Nah, dalam kesempatan kali ini kita akan membahas tentang cara menentukan himpunan penyelesaian dari Sistem Persamaan Linear serta Kuadrat (SPLK) menggunakan bagian kuadrat berbentuk tersirat yg bisa difak

Sistem persamaan linear dan kuadrat atau disingkat SPLK merupakan sistem persamaan yg terdiri atas sebuah persamaan linear serta sebuah persamaan kuadrat yg masing-masing bervariabel dua. SPLK dibedakan menjadi 2 jenis berdasarkan bentuk kuadratnya, yaitu SPLK menggunakan bagian kuadrat berbentuk eksplisit dan SPLK menggunakan bagian bagian kuadrat berbentuk tersirat. Secara generik, SPLK menggunakan bagian kuadrat berbentuk tersirat bisa dituliskan sebagai berikut. px + qy + r = 0 ……………. (bagian linear) ax2 + by2 + cxy + dx + ey + f = 0 ……………. (bagian kuadrat) Dengan a, b, c, d, e, f, p, q, dan r merupakan sapta-bilangan real. SPLK menggunakan bagian kuadrat yang berbentuk tersirat terdapat dua kemungkinan, yaitu: 1. SPLK bentuk implisit yg tidak dapat difaktorkan 2. SPLK bentuk implisit yang bisa difaktorkan Nah, pada kesempatan kali ini kita akan membahas tentang cara menentukan himpunan penyelesaian berdasarkan Sistem Persamaan Linear serta Kuadrat (SPLK) dengan bagian kuadrat be

Sistem persamaan linear serta kuadrat atau disingkat SPLK adalah sistem persamaan yg terdiri atas sebuah persamaan linear serta sebuah persamaan kuadrat yang masing-masing bervariabel 2. Contoh SPLK adalah menjadi berikut. y = dua–x ………………. Persamaan (1) y = x2–3x + dua ……… Persamaan (dua) Nah, pada kesempatan kali ini kita akan menyajikan formasi model soal dan pembahasan tentang sistem persamaan linear dan kuadrat (SPLK) menggunakan menggunakan aneka macam macam metode. Silahkan disimak baik-baik. Contoh Soal Sistem Persamaan Linear serta Kuadrat (SPLK) 1. Carilah himpunan penyelesaian SPLK berikut, kemudian gambarkan sketsa tafsiran geometerinya. y = x2–1 x–y = 3 Penyelesaian: Persamaan x–y = 3 dapat kita tulis ulang sebagai bentuk berikut. y = x–3 subtitusikan y = x–3 ke dalam persamaan y = x2–1 sehingga kita peroleh: ⇒x–tiga = x2–1 ⇒x–tiga = x2–1 ⇒x2–x–1 + 3 = 0 ⇒x2–x + 2 = 0 Persamaan kuadrat di atas sulit buat difaktorkan. Jika kita hitung nilai diskriminannya dengan nilai a =