Panduan Materi Belajar

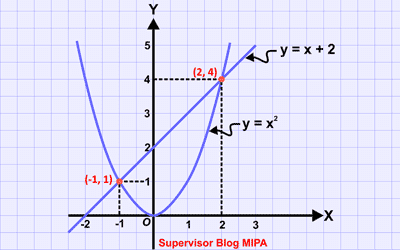
Sistem persamaan linear serta kuadrat atau disingkat SPLK adalah sistem persamaan yg terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yang masing-masing bervariabel 2. Berdasarkan ciri serta bagian bentuk kuadratnya, sistem persamaan linear dan kuadrat (SPLK) bisa dibedakan sebagai 2 jenis, yaitu SPLK dengan bagian kuadrat berbentuk eksplisit dan SPLK dengan bagian kuadrat berbentuk implisit. Nah, dalam kesempatan kali ini kita akan belajar tentang cara menentukan himpunan penyelesaian dari SPLK dengan bagian kuadratnya berbentuk eksplisit. Secara umum, bentuk baku dari SPLK dengan bagian kuadrat berbentuk eksplisit bisa ditulis sebagai berikut. y = ax + b ……………. (bagian linear) y = px2 + qx + r ……………. (bagian kuadrat) Dengan a, b, p, q, dan r merupakan sapta-bilangan real. Untuk tahu cara menentukan penyelesaian atau himpunan penyelesaian sistem persamaan linier dan kuadrat, simaklah SPLK ini dia. y = x + 2 ………. Bagian linear y = x2 …………… bagian kuadrat Subtitusikan

Dalam artikel tentang bentuk generik dan jenis-jenis persamaan kuadrat sudah dijelaskan bahwa persamaan kuadrat mempunyai bentuk generik ax2 + bx + c = 0 menggunakan a, b dan c adalah sapta real serta a ≠ 0. Persamaan ax2 + bx + c = 0 tadi bisa diselesaikan dengan cara memilih nilai pengganti x yang memenuhi persamaan itu. Dengan kata lain, jika nilai x disubtitusikan ke persamaan kuadrat maka hasilnya sama menggunakan nol. Nilai pengganti x yg memenuhi persamaan kuadrat ax2 + bx + c = 0 disebut penyelesaian atau akar berdasarkan persamaan kuadrat yang bersangkutan. Untuk menentukan akar-akar persamaan kuadrat, terdapat beberapa metode yang mampu digunakan, diantaranya merupakan menjadi berikut. #1 Memfaktorkan #dua Melengkapkan kuadrat sempurna #tiga Menggunakan rumus kuadrat (rumus ABC) #4 Menggambarkan sketsa grafik fungsi f(x) = ax2 + bx + c. Nah, pada kesempatan kali ini kita akan membahas mengenai cara gampang memilih akar-akar persamaan kuadrat menggunakan metode pemfaktoran.

Bentuk polinomial adalah bentuk suku banyak. Dalam bentuk spesifik, polinomial berderajat 2 biasa disebut bentuk kuadrat. Bentuk umum polinomial adalah sebagai berikut. anxn+ an–1xn–1+ an–2xn–dua+ … + a1x + a0 Pertidaksamaan yg akan kita bahas kali ini lebih ditekankan pada pertidaksamaan polinomial yg bisa difaktorkan. Bagaimana cara menyelesaikannya? Ikuti langkah-langkah berikut adalah. 1. Faktorkan suku poly itu. 2. Tentukan produsen nol suku poly. 3. Gambar garis bilangan yang memuat produsen nol. 4. Tentukan interval pada mana bernilai positif dan pada mana bernilai negatif. Tanda daerah terdekat (setelah melewati penghasil nol) berubah indikasi bila pangkat gasal, sedangkan bila pangkatnya genap, indikasi nir berubah. Misalkan: (x–a)3(x–b)(x–c)≥0 (x–a)2(x–b)(x–c)≥0 5. Tentukan daerah yang memenuhi problem tersebut. Sekarang agar kalian lebih paham mengenai bagaimana caranya memilih himpunan penyelesaian berdasarkan suatu pertidaksamaan polinomial, silahkan kalian simak beberap

Pertidaksamaan bentuk akar acapkali disebut jua pertidaksamaan irrasional, yaitu pertidaksamaan yg variabelnya masih ada dalam indikasi akar. Pertidaksamaan bentuk akar mempunyai 8 macam bentuk standar (generik) yaitu menjadi berikut. 1. √u(x) < a 1. √u(x) < √v(x) 2. √u(x)≤ a 2. √u(x)≤√v(x) 3. √u(x) > a 3. √u(x) > √v(x) 4. √u(x)≥ a 4. √u(x)≥√v(x) Dengan a ≥ 0, a ∈ R (a bilangan real positif atau nol). u(x) serta v(x) adalah fungsi-fungsi pada x dengan u(x) ≥ 0 dan v(x) ≥ 0. Misalkan kita mempunyai dua bilangan p serta q. ■Misalkan p = 5 maka 52 = 25 q = 8 maka 82 = 64 Tampak bahwa 0 < lima < 8 serta 52 < 82 ■Misalkan p = 1 maka 12 = 1 q = 3 maka 32 = 9 Tampak bahwa 0 < 1 < tiga dan 12 < 32 Berdasarkan contoh di atas, secara umum dapat dikatakan sebagai berikut. Jika p serta q ∈ R menggunakan 0 < p < q, maka p2 < q2 Dengan sifat tadi, kita dapat menuntaskan sistem pertidaksamaan bentuk akar dengan langkah-langkah menjadi berikut. 1. Kuadratkan ked

Pengertian serta Bentuk Umum SPKK Sistem persamaan kuadrat dan kuadrat atau disingkat menggunakan SPKK merupakan sistem persamaan yg terdiri atas dua persamaan kuadrat yg masing-masing memuat 2 variabel. SPKK mempunyai beberapa macam bentuk, namun dalam artikel ini kita akan lebih banyak membahas bentuk yang paling sederhana, yaitu ke 2 persamaan kuadrat berbentuk eksplisit. Bentuk umumnya merupakan sebagai berikut. y = ax2 + bx + c ……………. (bagian kuadrat pertama) y = px2 + qx + r ……………. (bagian kuadrat kedua) Dengan a, b, c, p, q, serta r adalah sapta-sapta real. Cara Menentukan Penyelesaian SPKK Misalkan terdapat SPKK menjadi berikut. y = x2 ……………………… pers. (1) y = x2– 2x ……………….. Pers. (dua) Subtitusikan persamaan (2) ke dalam persamaan (dua) sehingga diperoleh: ⇒ x2 = x2– 2x ⇒ 2x = x2– x2 ⇒ 2x = 0 ⇒ x = 0 Untuk x = 0 maka y = 0 Jadi, himpunan penyelesaian menurut sistem persamaan di atas adalah (0, 0). Secara geometris, anggota himpunan penyelesaian SPKK di atas merupakan titik pa