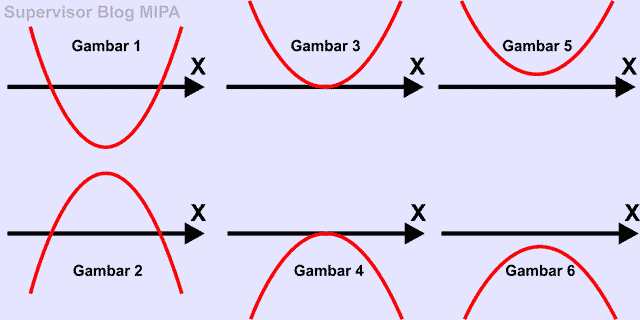
Cara Menentukan Persamaan Fungsi Kuadrat Berdasarkan Grafik Terbaru

Dalam artikel sebelumnya sudah dijelaskan tentang cara menggambar grafik fungsi kuadrat apabila persamaan atau rumus fungsi kuadrat tadi sudah diketahui. Sekarang yg sebagai pertanyaannya adalah bagaimana apabila gambar atau karakteristik-ciri grafik fungsi kuadrat sudah diketahui, dapatkah kita memilih persamaan fungsi kuadrat menurut grafik tadi? Tentu saja mampu. Apabila sketsa grafik suatu fungsi kuadrat diketahui, maka kita bisa menentukan rumus fungsi kuadrat itu. Proses demikian diklaim membangun atau menyusun fungsi kuadrat. Lalu tahukah kalian bagaimana caranya? Caranya sangat gampang sekali. Bisanya dalam soal telah ditetukan gambar grafik fungsi kuadrat atau liputan-fakta tentang grafik tersebut. Keterangan-liputan yg diketahui pada sketsa grafik fungsi kuadrat acapkali memiliki ciri-karakteristik atau sifat-sifat eksklusif. Ciri-ciri itu diantaranya merupakan sebagai berikut. #1 Grafik fungsi kuadrat memotong sumbu X pada A(x1, 0) dan B(x2, 0) dan melalui sebuah titik ek...