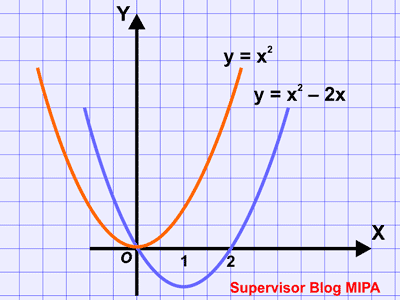
Contoh Soal dan Pembahasan SPKK Sistem Persamaan Kuadrat & Kuadrat Terbaru
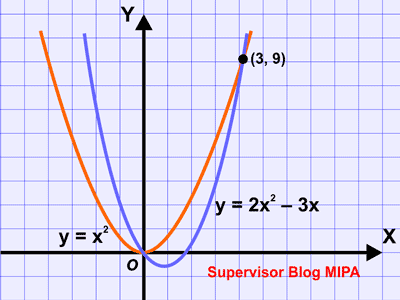
Sistem persamaan kuadrat serta kuadrat atau disingkat dengan SPKK merupakan sistem persamaan yang terdiri atas dua persamaan kuadrat yg masing-masing memuat 2 variabel. SPKK memiliki beberapa macam bentuk, namun pada artikel ini kita akan lebih poly membahas bentuk yang paling sederhana, yaitu kedua persamaan kuadrat berbentuk eksplisit. Bentuk biasanya merupakan menjadi berikut. y = ax2 + bx + c ……………. (bagian kuadrat pertama) y = px2 + qx + r ……………. (bagian kuadrat kedua) Dengan a, b, c, p, q, dan r merupakan sapta-sapta real. Secara umum, buat memperoleh penyelesaian SPKK dilakukan langkah-langkah sebagai berikut. Langkah 1: Subtitusikan bagian kuadrat persamaan pertama ke bagian kuadrat yang ke 2 atau kebalikannya sehingga diperoleh persamaan kuadrat baru. Langkah 2: Selesaikan persamaan kuadrat baru yang diperoleh pada langkah pertama. Langkah 3: Subtitusikan nilai x yang diperoleh pada langkah ke 2 ke persamaan pertama atau persamaan kedua. Untuk mempermudah perhitungan, silah...