Panduan Materi Belajar

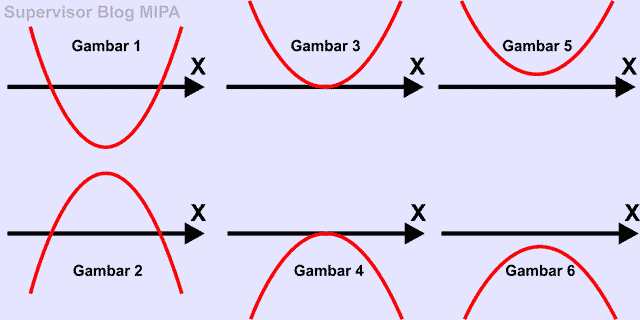
Dalam matematika, jenis-jenis fungsi ada tujuh macam, dua di antaranya adalah fungsi linear dan fungsi kuadrat. Fungsi linear atau fungsi polinom (sukubanyak) berderajat satu pada variabel x merupakan suatu bentuk fungsi f(x) = ax + b dimana a, b ∈ R  serta a ≠ 0 buat seluruh x dalam wilayah asalnya. Bentuk grafik fungsi linear dalam bidang Cartesian merupakan berupa garis lurus. Lalu bagaimana dengan bentuk umum serta grafik fungsi kuadrat? Untuk menjawab pertanyaan tadi, silahkan kalian pelajari artikel ini menggunakan seksama. Bentuk Umum Fungsi Kuadrat Untuk tahu definisi atau pengertian fungsi kuadrat serta bentuk umumnya, perhatikan beberapa contoh fungsi ini dia. •f(x) = x2– 1 •f(x) = 2x2– 6x •f(x) = x2– 4x + 8 •f(x) = –3x2 + 4x – 9 Dari keempat contoh fungsi di atas, pangkat tertinggi variabel x pada tiap-tiap fungsi sama menggunakan 2. Fungsi yang memiliki karakteristik seperti itu disebut fungsi kuadrat pada variabel x. Dengan demikian, bentuk generik fungsi kuadrat bisa d

Coba kalian perhatikan beberapa bentuk pertidaksamaan berikut ini. ■x2– 4x + 3 < 0 ■x2 + 2x – lima ≤ 0 ■2x2– 11x + 5 > 0 ■3x2– x – dua ≥ 0 Keempat bentuk pertidaksamaan pada atas memuat variabel x berpangkat 2. Pertidaksamaan yg bentuknya demikian diklaim menggunakan pertidaksamaan kuadrat dalam variabel x. Dalam matematika, bentuk baku pertidaksamaan kuadrat pada variabel x terdapat empat macam, yaitu ■ax2 + bx + c < 0 (kurang dari) ■ax2 + bx + c ≤ 0 (kurang dari sama menggunakan) ■ax2 + bx + c > 0 (lebih dari) ■ax2 + bx + c ≥ 0 (lebih dari sama dengan) Dengan a, b serta c merupakan bilangan real serta a ≠ 0. Penyelesaian atau himpunan penyelesaian dari pertidaksamaan kuadrat dalam variabel x bisa ditentukan dengan 2 cara, yaitu menggunakan menggunakan metode berikut adalah. 1. Sketsa grafik fungsi kuadrat 2. Garis bilangan Nah pada kesempatan kali ini, kita akan belajar tentang cara memilih himpunan penyelesaian pertidaksamaan kuadrat dengan menggunakan sketsa grafik fun

Pengertian SPLK Misalkan kita mempunyai nilai x = 0 serta y = 2, maka nilai-nilai tadi memenuhi sistem persamaan berikut. y = dua – x y = x2– 3x + 2 Dikatakan demikian karena menggunakan mensubtitusikan x = 0 serta y = 2 ke masing-masing persamaan, diperoleh pernyataan yg sahih, yaitu: ■x = 0 dan y = dua, maka: ⇒ y = dua – x ⇒ dua = dua – 0 ⇒ dua = 2 …………… (benar) ■x = 0 dan y = dua, maka: ⇒ y = x2– 3x + 2 ⇒ dua = (0)dua– 3(0) + 2 ⇒ dua = 0 – 0 + 2 ⇒ dua = 2 …………… (benar) Sekarang coba kita selidiki apakah x = 2 serta y = 0 pula memenuhi sistem persamaan linear dan kuadrat y = dua – x serta y = x2– 3x + 2. Perhatikan perhitungan ini dia. ■x = 2 serta y = 0, maka: ⇒ y = dua – x ⇒ 0 = dua – 2 ⇒ 0 = 0 …………… (sahih) ■x = 2 serta y = 0, maka: ⇒ y = x2– 3x + 2 ⇒ 0 = (2)dua– tiga(2) + 2 ⇒ 0 = 4 – 6 + 2 ⇒ 0 = –2 + 2 ⇒ 0 = 0 …………… (sahih) Dengan demikian bisa dikatakan bahwa pasangan berurutan (0, dua) dan (2, 0) merupakan penyelesaian menurut sistem persamaan: y = dua – x y = x2– 3x + 2 Himpu

Pertidaksamaan x2 + 3x + 1 < 0, 2x2 + 4x – 5 ≥ 0, atau x2– 5x + 4 > 0 adalah model-contoh pertidaksamaan kuadrat. Secara generik, pertidaksamaan kuadrat merupakan pertidaksamaan satu variabel berderajat 2, dengan bentuk umum sebagai berikut. ■ax2 + bx + c < 0 ■ax2 + bx + c ≤ 0 ■ax2 + bx + c > 0 ■ax2 + bx + c ≥ 0 Dengan a, b, c sapta real serta a ≠ 0. Pertidaksamaan kuadrat bisa diselesaikan menggunakan beberapa cara, pada antaranya merupakan sebagai berikut. 1. Sketsa grafik fungsi kuadrat 2. Garis bilangan Nah, dalam kesempatan kali ini kita akan belajar mengenai cara memilih himpunan penyelesaian berdasarkan suatu pertidaksamaan kuadrat menggunakan 2 metode pada atas, yaitu sketsa grafik fungsi kuadrat serta garis sapta. Untuk itu, silahkan kalian simak baik-baik penjelasan berikut in. Selamat belajar dan semoga mampu paham. Menyelesaikan Pertidaksamaan Kuadrat menggunakan Grafik Fungsi Kuadrat Sebuah fungsi kuadrat ditentukan menggunakan rumus f(x) = −x2 + 4x – tiga. Gr

Pengertian Fungsi Konsep fungsi atau pemetaan merupakan galat satu konsep yg sangat mendasar dalam mempelajari matematika. Banyak sekali problem dalam kehidupan sehari-hari yang solusinya memakai fungsi. Sebagai model, hubungan antara anak didik-siswi kelas X Sekolah Menengah Atas Negeri tiga Antah Berantah menggunakan jenis kelaminnya. Lalu tahukah kalian apa yg dimaksud menggunakan fungsi atau pemetaan? Untuk mampu tahu definisi fungsi, silahkan kalian perhatikan gambar ini dia. Pada gambar pada atas, diperlihatkan diagram panah suatu relasi berdasarkan himpunan A ke himpunan B, dengan A = a, b, c serta B = p, q, r, s. Tampak bahwa setiap anggota himpunan A dihubungkan dengan tepat pada satu anggota himpunan B. Relasi yang memiliki karakteristik-karakteristik tadi dinamakanfungsi atau pemetaan. Dengan demikian bisa kita simpulkan pengertian menurut fungsi atau pemetaan yaitu sebagai berikut. Fungsi atau pemetaan adalah rekanan himpunan A ke himpunan B yang memasangkan setiap anggota

Dalam artikel sebelumnya, telah dijelaskan mengenai cara menentukan himpunan penyelesaian pertidaksamaan kuadrat dengan memakai grafik fungsi kuadrat atau grafik parabola. Nah, dalam artikel ini kita akan belajar tentang bagaimana caranya menentukan penyelesaian pertidaksamaan kuadrat dengan menggunakan diagram garis sapta. Sebagai contoh, kita akan memilih himpunan penyelesaian pertidaksamaan kuadrat x2– 4x + 3 < 0 menggunakan memakai metode garis sapta. Langkah-langkah yg perlu kalian lakukan adalah menjadi berikut. Langkah #1 Tentukanlah nilai-nilai nol (bila ada) dari bagian ruas kiri pertidaksamaan kuadrat. Caranya merupakan menggunakan menggunakan metode pemfaktoran yaitu sebagai berikut. ⇔ x2– 4x + 3 = 0 ⇔ (x – 1)(x – 3) = 0 ⇔ x = 1 atau x = 3 Langkah #2 Gambarlah nilai-nilai nol yg diperoleh pada langkah #1 dalam bentuk diagram garis sapta. Dan perlu kalian perhatikan, bahwa nilai-nilai nol tadi membagi garis menjadi 3 interval (selang), yaitu x < 1, 1 < x < tiga