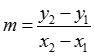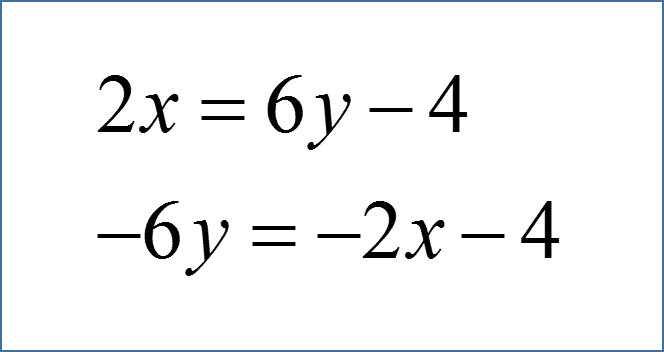Panduan Materi Belajar

Garis lurus memang ditandakan sang adanya gradien atau kemiringannya. Dan kini kita akan membahas galat satu bentuk soal yg herbi gradien. Ini merupakan variasi lainnya. Mari lihat lagi soalnya.. Contoh soal : 1. Suatu garis lurus melewati titik (2,6) serta (1,a) serta garis ini memiliki gradien (m) = tiga. Berapakah nilai a? Langkah 1 → Analisa soal Yang diketahui hanyalah gradien garis bersama 2 titiknya. Jadi,, Soal misalnya ini hanya cukup diselesaikan menggunakan rumus gradien garis saat dilewati 2 butir titik. Masih jangan lupa rumus gradien garisnya? Langkah 2 → Mencari jawabannya Rumus buat mencari gradien adalah sebagai berikut. Bagaimana memilih nilai y dan x nya? Lihat lagi dibawah ini.. Jelas ya? Bagaimana apabila (1,a) digunakan menjadi x1 dan y1? Hasilnya sama saja.. Anda bebas menentukan mana yang pertama serta mana yg kedua.. Sekarang kita tambahkan ke rumusnya.. Ganti m menggunakan 3 Masukkan y2, y1, x2, x1 sesuai dengan yg sudah dijelaskan diatas. Untuk menghilangkan

Dalam soal diketahui bila kedua garis tersebut saling tegak lurus serta kita akan menggunakan rumus yang bekerjasama dengannya. Lebih lengkapnya langsung dicermati pada model soal.. Soal : 1. Garis "m" tegak lurus menggunakan garis 2x - 6y = tiga. Berapakah gradien garis "m"? Langkah-langkah mengerjakan soal ini menjadi berikut : Mencari gradien garis 2x - 6y = 3 Menggunakan rumus gradien saling tegak lurus, kita cari gradien garis m Mencari gradien garis 2x - 6y = 3 Untuk mendapatkan gradien garis ini, maka variabel y wajib berada sendiri di ruas kiri dan nomor di depannya harus 1. Mari kita kerjakan.. Caranya merupakan : pindahkan 2x ke ruas kanan menjadi -2x variabel y sekarang telah sendiri di ruas kiri agar nomor di depan y sebagai 1, maka semuanya wajib dibagi menggunakan -6 (sinkron angka yang ada pada depan variabel y ketika ini) akhirnya kita mendapatkan variabel "y" yg angka depannya 1 Ketika nomor di depan y telah 1, maka : gradien garisnya mer

Rumus Persamaan Garis Lurus Beserta Contoh Soal - Dalam pelajaran Matematika terdapat materi pembelajaran tentang rumus persamaan garis lurus. Apa itu persamaan garis lurus? Persamaan garis lurus tak jarang diklaim menjadi persamaan linier yg adalah persamaan yang terdiri dari satu variabel atau lebih. Persamaan garis lurus selalu berkaitan menggunakan gradien. Tanpa adanya gradien maka persamaannya tidak bisa diketahui, kecuali berpotongan antara kedua titik. Pada kesempatan kali ini aku akan menjelaskan mengenai rumus persamaan garis lurus beserta model soal persamaan garis lurus. Untuk detail dapat anda simak dibawah ini. Rumus Persamaan Garis Lurus Beserta Contoh Soal Persamaan garis lurus adalah perbandingan koordinat x menggunakan koordinat y yg yang terletak antara dua titik dalam garis. Dalam rumus persamaan garis lurus dan model soal persamaan garis lurus masih ada gradien didalamnya. Apa itu gradien? Gradien ialah perbandingan antara komponen x dengan komponen y yang akan

Setelah sebelumnya membahas persamaan garis yang tegak lurus, sekarang saya akan membahas bagaimana cara mencari persamaan garis yang sejajar. Baca pula : Mencari Gradien Garis L yg Tegak Lurus Garis 3x - y = 4 Mencari Gradien Garis K yg Tegak Lurus Dengan Garis 4x - 2y = 5 Prosesnya lebih gampang dibandingkan dengan persamaan garis lurus. Nanti akan dijelaskan lagi secara lebih jelas mengapa mencari persamaan garis seperti ini lebih enteng. Contoh soal  1. Suatu garis K melewati titik (2,3) serta sejajar dengan garis N yg mempunyai persamaan 2y + 3x = 4. Bagaimanakah persamaan garis K tersebut? Langkah buat mendapatkan jawaban menurut soal ini adalah : mencari gradien garis menurut 2y + 3x = 4 karena sejajar, maka gradien garis K sama menggunakan gradien garis N Setelah itu tambahkan datanya ke rumus persamaan garis. Nah, seperti itulah langkah-langkah yg sanggup kita tempuh. Mencari gradien garis N menggunakan persamaan 2y + 3x = 4. Untuk menerima gradiennya, maka y harus sendiri di

Mencari gradien menurut suatu persamaan garis yg sudah diketahui mudah sekali. Yang penting tahu konsepnya, maka gradien bisa diperoleh. Nah, dibawah ini akan diberikan sedikit model soal bagaimana cara mencari gradien menurut suatu garis lurus yg diketahui persamaannya.. Contoh soal : 1. Garis "a" mempunyai persamaan 2x + y = 4. Berapakah gradien menurut garis a? Untuk mendapatkan gradien berdasarkan suatu garis lurus yang telah diketahui persamaannya, sanggup diperhatikan cara berikut.. Caranya : buat variabel "y" berada sendiri di sebelah kiri koefisien "y" haruslah 1 gradien merupakan angka pada depan variabel "x" Biar lebih dipahami, kita perhatikan contoh soalnya saja.. Persamaan garisnya adalah 2x + y = 4 y terdapat sahabat pada sebelah kiri, yaitu 2x 2x harus dipindahkan ke ruas kanan agar y sendiri pada ruas kiri 2x pindah sebagai akibatnya sebagai (-2x) 2x + y = 4 y = -2x + 4 Sekarang perhatikan apakah "y" koefisiennya telah

Pada artikel sebelumnya, saya pula membahas bagaimana cara mencari gradien suatu garis lurus jika diketahui 2 butir titik yang dilaluinya. Baca disini : Contoh soal cara mencari gradien jika diketahui 2 buah titik koordinatnya Dan pada kesempatan kali ini, akan balik diulas menggunakan memakai contoh tidak sinkron sebagai akibatnya sanggup memberikan pemahaman yang lebih mendalam lagi. Ok, cek soalnya.. Mari pribadi saja kita lihat ke contoh soalnya, rumus apa yg dipakai dan bagaimana cara menentukan hal-hal yang diminta dalam rumus.. Contoh soal : 1. Sebuah garis lurus melewati dua buah titik yaitu (-2, -5) serta (8,1). Berapakah gradien dari garis tersebut? Masih ingat rumus buat mencari gradien  (m) jika terdapat dua titik yang diketahui? Nah, misalnya ini rumusnya.. Sekarang kita tentukan dulu titik-titik dari x₁ , y₁ serta x₂ , y₂ . Titik pertama (-dua, -lima) : x₁ = -2 y₁ = -5 Titik ke 2 (8,1) x₂ = 8 y₂ = 1 Masukkan nilai-nilai tersebut ke dalam rumus yg sudah terdapat.. Nah, gr

Nah disini kita akan mencari nilai gradien garis L yg tegak lurus menggunakan satu garis lain. Dan sebelum menemukan gradien L, kita wajib menerima gradien garis yg telah diketahui. Nanti akan dipakai sifat dua gradien yg saling tegak lurus serta bagaimana interaksi keduanya. Cek soalnya.. Ok,  terdapat sedikit soal yg bisa diperhatikan buat mencari jawaban berdasarkan problem ini. Yuk langsung lihat soalnya.. Contoh soal : 1. Suatu garis L tegak lurus dengan garis 3x - y = 4. Berapakah gradien berdasarkan garis L tadi? Berarti dalam soal ada 2 buah garis lurus, yg pertama adalah garis L serta yang ke 2 merupakan garis dengan persamaan 3x - y = 4. gradien garis L kita sebut dengan "m₁" gradien garis 3x - y = 4 kita sebut menggunakan "m₂" Sekarang kita lihat interaksi keduanya.. Kalau terdapat 2 butir garis yg saling tegak lurus, maka hasil kali kedua gradiennya merupakan minus satu (-1) serta sanggup ditulis : m₁ × m₂ = -1 Sifat inilah yg akan dipakai buat memilih

Untuk menerima output menurut soal seperti ini, kita mampu mencari persamaan garisnya terlebih dahulu. Caranya adalah menggunakan memakai 2 butir titik yg telah diketahui. Tapi jika malas mencari persamaan garisnya, nir masalah kok.. Ada satu cara lagi yg jauh lebih cepat dibandingkan wajib mencari persamaan garisnya. Jadi tidak perlu membuang ketika hiperbola. Ok, ayo lihat lagi soalnya.. Contoh soal : 1. Diketahui 3 butir titik (1,tiga), (-2, -tiga) dan (a,lima) berada pada satu garis lurus. Berapakah nilai menurut a? Mari kita perhatikan penerangan dibawah ini!! Analisa soal Nah, telah dijelaskan pada soal dengan terperinci benderang bahwa ketiga titik ini berada pada satu garis lurus. Jika terdapat buku kotak-kotak, maka tinggal tentukan saja titik-titiknya serta tariklah garis lurus. Panjangkan garisnya hingga mencapai nilai "sumbu y" sama dengan 5. Kemudian lihatlah berapa nilai x-nya. Itu kalau terdapat kitab kotak-kotak, jikalau tidak ada kita mampu menghitungnya. Ca

Gradien mampu ditemukan dalam soal mencari persamaan garis lurus serta menjadi utama bahasan materi matematika di SMP atau SMA. Gradien mampu diartikan kemiringan garis lurus tadi. Yap.. Gradien hanya ditemukan dalam garis lurus.. Untuk garis melengkung misalnya parabola atau lingkaran, nir sanggup dicari gradiennya. Gradien hanya sanggup dicari ketika bersinggungan dengan garis lurus saja atau disatu titik. Arti gradien ⅘ Trus, apa ya arti menurut gradien itu bila dinyatakan dengan angka? Kita akan merogoh contoh gradien (m) = ⅘. Tapi sebelumnya, coba perhatikan dulu gambar berikut adalah.. Garis berwarna merah yg kita lihat posisinya. Dilihat menurut titik A Kita lihat dulu menurut titik A. Titik ini akan dijadikan patokan buat menentukan titik B dengan memakai gradien yg sudah diberikan. Arti berdasarkan gradien ⅘ adalah sebagai berikut : Angka 4 dalam ⅘ merupakan titik berkecimpung sebesar 4 langkah ke kanan atau kekiri pada sumbu x. Angka 5 pada ⅘ merupakan titik berkecimpung seb

Untuk melihat perpaduan soal-soal tentang gradien garis, silahkan cek di link berikut ini : ====>>> "Kumpulan soal-soal gradien garis lurus" Ok, kini kita langsung masuk ke contoh soalnya : 1. Suatu garis lurus mempunyai persamaan 2x = 6y -4, berapakah gradien garisnya??? Jawab : Persamaan ini wajib diubah dahulu supaya memenuhi y = mx + c Variabel "y" pada persamaan diatas masih berada pada kanan tanda (=), maka wajib dipindah dahulu serta di depan variabel "y" nir boleh terdapat angka selain 1. Pada persamaan diatas, "y" sudah berada pada kiri (=) tapi masih ada nomor -6 disana. Jadi wajib dihilangkan menggunakan cara membaginya menggunakan -6 juga. Nah, variabel "y" sudah sendiri serta tidak ada nomor pada depannya (atau hanya terdapat nomor 1. Ingat 1y = y). Jadi gradien garis lurus persamaan diatas merupakan angka di depan variable "x", yaitu 1/3. gradien (m) = 1/3. Anda pula sanggup membaca konsep umum mengenai