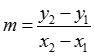Panduan Materi Belajar

Rumus Persamaan Garis Lurus Beserta Contoh Soal - Dalam pelajaran Matematika terdapat materi pembelajaran tentang rumus persamaan garis lurus. Apa itu persamaan garis lurus? Persamaan garis lurus tak jarang diklaim menjadi persamaan linier yg adalah persamaan yang terdiri dari satu variabel atau lebih. Persamaan garis lurus selalu berkaitan menggunakan gradien. Tanpa adanya gradien maka persamaannya tidak bisa diketahui, kecuali berpotongan antara kedua titik. Pada kesempatan kali ini aku akan menjelaskan mengenai rumus persamaan garis lurus beserta model soal persamaan garis lurus. Untuk detail dapat anda simak dibawah ini. Rumus Persamaan Garis Lurus Beserta Contoh Soal Persamaan garis lurus adalah perbandingan koordinat x menggunakan koordinat y yg yang terletak antara dua titik dalam garis. Dalam rumus persamaan garis lurus dan model soal persamaan garis lurus masih ada gradien didalamnya. Apa itu gradien? Gradien ialah perbandingan antara komponen x dengan komponen y yang akan

Setelah sebelumnya membahas persamaan garis yang tegak lurus, sekarang saya akan membahas bagaimana cara mencari persamaan garis yang sejajar. Baca pula : Mencari Gradien Garis L yg Tegak Lurus Garis 3x - y = 4 Mencari Gradien Garis K yg Tegak Lurus Dengan Garis 4x - 2y = 5 Prosesnya lebih gampang dibandingkan dengan persamaan garis lurus. Nanti akan dijelaskan lagi secara lebih jelas mengapa mencari persamaan garis seperti ini lebih enteng. Contoh soal  1. Suatu garis K melewati titik (2,3) serta sejajar dengan garis N yg mempunyai persamaan 2y + 3x = 4. Bagaimanakah persamaan garis K tersebut? Langkah buat mendapatkan jawaban menurut soal ini adalah : mencari gradien garis menurut 2y + 3x = 4 karena sejajar, maka gradien garis K sama menggunakan gradien garis N Setelah itu tambahkan datanya ke rumus persamaan garis. Nah, seperti itulah langkah-langkah yg sanggup kita tempuh. Mencari gradien garis N menggunakan persamaan 2y + 3x = 4. Untuk menerima gradiennya, maka y harus sendiri di

Model soal seperti ini sanggup dikerjakan menggunakan mencari gradiennya terlebih dahulu. Nah, yuk kita lihat lagi bagaimana cara menuntaskan persoalan misalnya ini disertai dengan langkah-langkah lengkapnya.. Contoh soal : 1. Suatu garis lurus melewati 2 butir titik (dua, -1) dan (3, 2). Carilah persamaan garis lurus tersebut? Mari kita kerjakan soalnya.. Langkah 1 ⇒ analisa soal Untuk mendapatkan persamaan garis lurus dari dua butir titik, maka terdapat 2 langkah yg harus dilakukan. Pertama → Cari gradien garisnya Kedua    → Cari persamaan garis. Nah, itulah langkah yg akan kita lakukan.. Langkah 2 ⇒ Mencari gradien garis Rumus buat gradien garis adalah seperti dibawah ini. m = gradien garis Untuk ke 2 titik yg diketahui, kemudian dipecah menjadi  x1, y1, x2 dan y2. Titik pertama sebagai x1 serta y1 titik ke 2 sebagai x2 dan y2 Sekarang tambahkan semua titik itu ke dalam rumus gradien. Baca Juga Mencari Persamaan Garis Lurus Jika Diketahui 2 Titik Cara Mencari Persamaan Garis Lurus

Untuk menerima output menurut soal seperti ini, kita mampu mencari persamaan garisnya terlebih dahulu. Caranya adalah menggunakan memakai 2 butir titik yg telah diketahui. Tapi jika malas mencari persamaan garisnya, nir masalah kok.. Ada satu cara lagi yg jauh lebih cepat dibandingkan wajib mencari persamaan garisnya. Jadi tidak perlu membuang ketika hiperbola. Ok, ayo lihat lagi soalnya.. Contoh soal : 1. Diketahui 3 butir titik (1,tiga), (-2, -tiga) dan (a,lima) berada pada satu garis lurus. Berapakah nilai menurut a? Mari kita perhatikan penerangan dibawah ini!! Analisa soal Nah, telah dijelaskan pada soal dengan terperinci benderang bahwa ketiga titik ini berada pada satu garis lurus. Jika terdapat buku kotak-kotak, maka tinggal tentukan saja titik-titiknya serta tariklah garis lurus. Panjangkan garisnya hingga mencapai nilai "sumbu y" sama dengan 5. Kemudian lihatlah berapa nilai x-nya. Itu kalau terdapat kitab kotak-kotak, jikalau tidak ada kita mampu menghitungnya. Ca

Sebelumnya sudah dibahas mengenai mencari suatu gradien yg sejajar menggunakan suatu garis lain. Silahkan baca disini :   Baca jua   : Soal mencari gradien garis yang sejajar dengan garis lain Dan kini .. Giliran membahas soal mencari gradien garis yg tegak lurus dengan garis lainnya.. Ok, eksklusif ke soalnya.. Contoh soal : 1. Garis "m" tegak lurus dengan garis "n" yg mempunyai persamaan y = 4x -3. Berapakah gradien berdasarkan garis m?? Diketahui : m tegak lurus n persamaan garis n ==>> y = 4x - 3 Ditanya : Gradien garis "m"...?? Jawab : Karena yang diketahui adalah garis "n", maka kita cari dulu gradiennya. Tapi sebelumnya, silahkan baca dulu bagaimana mencari gradien suatu garis pada 2 artikel berikut ya!! Baca : Konsep umum mencari gradien suatu garis lurus Contoh soal mencari gradien garis lurus Setelah mengetahui cara mencari gradien suatu garis lurus, maka kita mampu menghitung gradien garis "n". y = 4x -3 Karena y tela

Untuk persamaan garis yg melewati dua butir titik, ada rumus langsung yg bisa digunakan. Itulah yang kita pakai. Untuk lebih jelasnya, kita kerjakan saja soalnya.. Soal : 1. Suatu garis lurus melewati 2 buah titik, yaitu (dua,1) dan (-1,4). Bagaimanakah persamaan garisnya? Rumus yang dipakai merupakan seperti ini.. Kita tentukan titik-titiknya. Titik pertama (2,1) x₁ = 2 y₁ = 1 Titik kedua (-1,4) x₂ = -1 y₂ = 4 Sekarang tambahkan titik-titiknya ke pada rumus. Sekarang dikalikan silang : -tiga menggunakan (y-1) 3 dengan (x-dua) Untuk membuka kurung : kalikan -3 menggunakan y hasilnya -3y, kalikan -tiga dengan -1, hasilnya +3 kalikan tiga dengan x hasilnya 3x, kalikan tiga menggunakan -dua hasilnya -6 Kemudian : pindahkan -3y ke ruas kanan agar sebagai positif, +3y pindahkan -6 ke ruas kiri sebagai +6 Sekarang kita sanggup sederhanakan lagi.. bagi tiga semuanya. Jadi persamaan garis berdasarkan ke 2 titik diatas adalah "y + x = 3" Atau, pindahkan x ke ruas kiri sebagai akibatn

Halo.. Selamat datang pulang pada blog ini.. Blog yg membahas soal-soal matematika disertai menggunakan penjelasan singkatnya. Dan.. Kali ini kita akan membahas soal tentang persamaan garis.. Yuk langsung saja ke soalnya.. Contoh soal : 1. Sebuah garis lurus melalui titik koordinat (dua,5) serta mempunyai gradien 4. Apakah persamaan garis tadi?? Diketahui : Koordinat (dua,5) gradien (m) = 4 Ditanya : Persamaan garisnya..? Jawab : Rumus buat mencari persamaan garis seperti ini adalah : Kemudian, kita tentukan dulu x1 dan y1 : Nah, sekarang saatnya buat mencari persamaan garisnya.. Ok.. Hasilnya telah ketemu ya.. Persamaan garis yg dimaksud sudah diperoleh, yaitu  y = 4x - tiga

Garis lurus memang ditandakan sang adanya gradien atau kemiringannya. Dan kini kita akan membahas galat satu bentuk soal yg herbi gradien. Ini merupakan variasi lainnya. Mari lihat lagi soalnya.. Contoh soal : 1. Suatu garis lurus melewati titik (2,6) serta (1,a) serta garis ini memiliki gradien (m) = tiga. Berapakah nilai a? Langkah 1 → Analisa soal Yang diketahui hanyalah gradien garis bersama 2 titiknya. Jadi,, Soal misalnya ini hanya cukup diselesaikan menggunakan rumus gradien garis saat dilewati 2 butir titik. Masih jangan lupa rumus gradien garisnya? Langkah 2 → Mencari jawabannya Rumus buat mencari gradien adalah sebagai berikut. Bagaimana memilih nilai y dan x nya? Lihat lagi dibawah ini.. Jelas ya? Bagaimana apabila (1,a) digunakan menjadi x1 dan y1? Hasilnya sama saja.. Anda bebas menentukan mana yang pertama serta mana yg kedua.. Sekarang kita tambahkan ke rumusnya.. Ganti m menggunakan 3 Masukkan y2, y1, x2, x1 sesuai dengan yg sudah dijelaskan diatas. Untuk menghilangkan

Dalam soal diketahui bila kedua garis tersebut saling tegak lurus serta kita akan menggunakan rumus yang bekerjasama dengannya. Lebih lengkapnya langsung dicermati pada model soal.. Soal : 1. Garis "m" tegak lurus menggunakan garis 2x - 6y = tiga. Berapakah gradien garis "m"? Langkah-langkah mengerjakan soal ini menjadi berikut : Mencari gradien garis 2x - 6y = 3 Menggunakan rumus gradien saling tegak lurus, kita cari gradien garis m Mencari gradien garis 2x - 6y = 3 Untuk mendapatkan gradien garis ini, maka variabel y wajib berada sendiri di ruas kiri dan nomor di depannya harus 1. Mari kita kerjakan.. Caranya merupakan : pindahkan 2x ke ruas kanan menjadi -2x variabel y sekarang telah sendiri di ruas kiri agar nomor di depan y sebagai 1, maka semuanya wajib dibagi menggunakan -6 (sinkron angka yang ada pada depan variabel y ketika ini) akhirnya kita mendapatkan variabel "y" yg angka depannya 1 Ketika nomor di depan y telah 1, maka : gradien garisnya mer

Dalam perhitungan matematika dan pada kehidupan sehari-hari, acapkali suatu kasus dapat diterjemahkan ke pada contoh matematika yg berbentuk sistem persamaan. Sistem persamaan yang diperoleh itu bisa berbentuk SPLDV , SPLTV, atau SPLK. Penyelesaian SPLDV, SPLTV, serta SPLK yg sudah dibahas pada artikel-artikel sebelumnya memegang peranan penting pada pemecahan masalah tersebut. Langkah pertama yang diharapkan merupakan kita wajib mampu mengidentifikasi bahwa karakteristik kasus yang akan diselesaikan berkaitan menggunakan sistem persamaan (SPLDV, SPLTV , atau SPLK). Setelah masalahnya teridentifikasi, penyelesaian selanjutnya melalui langkah-langkah sebagai berikut. 1. Nyatakan besaran yg terdapat dalam masalah sebagai variabel (dilambangkan menggunakan alfabet -huruf) sistem persamaan. 2. Rumuskan sistem persamaan yg merupakan model matematika dari perkara. 3. Tentukan penyelesaian dari model matematika sistem persamaan yang diperoleh pada langkah 2. 4. Tafsirkan terhadap hasil yang