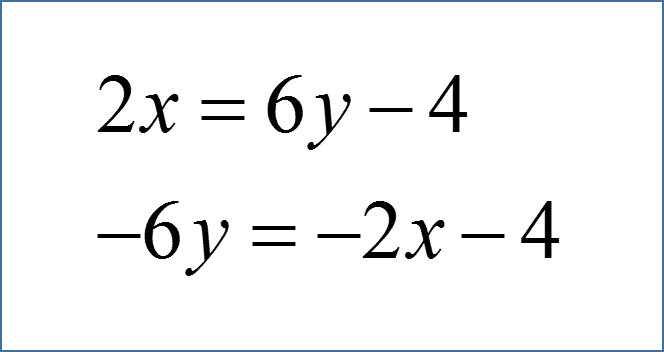Panduan Materi Belajar

Pada artikel sebelumnya, saya pula membahas bagaimana cara mencari gradien suatu garis lurus jika diketahui 2 butir titik yang dilaluinya. Baca disini : Contoh soal cara mencari gradien jika diketahui 2 buah titik koordinatnya Dan pada kesempatan kali ini, akan balik diulas menggunakan memakai contoh tidak sinkron sebagai akibatnya sanggup memberikan pemahaman yang lebih mendalam lagi. Ok, cek soalnya.. Mari pribadi saja kita lihat ke contoh soalnya, rumus apa yg dipakai dan bagaimana cara menentukan hal-hal yang diminta dalam rumus.. Contoh soal : 1. Sebuah garis lurus melewati dua buah titik yaitu (-2, -5) serta (8,1). Berapakah gradien dari garis tersebut? Masih ingat rumus buat mencari gradien  (m) jika terdapat dua titik yang diketahui? Nah, misalnya ini rumusnya.. Sekarang kita tentukan dulu titik-titik dari x₁ , y₁ serta x₂ , y₂ . Titik pertama (-dua, -lima) : x₁ = -2 y₁ = -5 Titik ke 2 (8,1) x₂ = 8 y₂ = 1 Masukkan nilai-nilai tersebut ke dalam rumus yg sudah terdapat.. Nah, gr

Nah disini kita akan mencari nilai gradien garis L yg tegak lurus menggunakan satu garis lain. Dan sebelum menemukan gradien L, kita wajib menerima gradien garis yg telah diketahui. Nanti akan dipakai sifat dua gradien yg saling tegak lurus serta bagaimana interaksi keduanya. Cek soalnya.. Ok,  terdapat sedikit soal yg bisa diperhatikan buat mencari jawaban berdasarkan problem ini. Yuk langsung lihat soalnya.. Contoh soal : 1. Suatu garis L tegak lurus dengan garis 3x - y = 4. Berapakah gradien berdasarkan garis L tadi? Berarti dalam soal ada 2 buah garis lurus, yg pertama adalah garis L serta yang ke 2 merupakan garis dengan persamaan 3x - y = 4. gradien garis L kita sebut dengan "m₁" gradien garis 3x - y = 4 kita sebut menggunakan "m₂" Sekarang kita lihat interaksi keduanya.. Kalau terdapat 2 butir garis yg saling tegak lurus, maka hasil kali kedua gradiennya merupakan minus satu (-1) serta sanggup ditulis : m₁ × m₂ = -1 Sifat inilah yg akan dipakai buat memilih

Soal yg seperti sudah pernah saya bahas pada artikel dalam dalam blog ini. Silahkan baca dalam link berikut ya.. Baca juga : Mencari gradien garis L yg tegak lurus dengan garis 3x - y = 4 Soal yg ada dalam artikel ini akan semakin melengkapi soal tersebut dan mampu membantu anda semakin tahu cara mencari gradien dua garis yg saling tegak lurus. Mari kita mulai berdasarkan soal pertama.. Contoh soal : 1. Garis K tegak lurus dengan garis 4x - 2y = 5. Berapakah gradien menurut garis K tadi? Dalam soal diketahui ada dua butir garis yg saling tegak lurus. pertama adalah garis K, yang gradiennya kita sebut menggunakan "m₁" kedua adalah garis 4x - 2y = lima, gradiennya kita sebut menggunakan "m₂" Apa kunci menurut 2 garis yg saling tegak lurus? Hasil kali kedua gradiennya adalah -1. Inilah yang akan dipakai buat mencari gradien menurut garis K. m₁ × m₂ = -1 Tapi kita belum memahami gradien garis 4x - 2y = 5. Nah, inilah yang harus dicari terlebih dahulu.. Caranya : tempat

Sebelumnya sudah dibahas mengenai mencari suatu gradien yg sejajar menggunakan suatu garis lain. Silahkan baca disini :   Baca jua   : Soal mencari gradien garis yang sejajar dengan garis lain Dan kini .. Giliran membahas soal mencari gradien garis yg tegak lurus dengan garis lainnya.. Ok, eksklusif ke soalnya.. Contoh soal : 1. Garis "m" tegak lurus dengan garis "n" yg mempunyai persamaan y = 4x -3. Berapakah gradien berdasarkan garis m?? Diketahui : m tegak lurus n persamaan garis n ==>> y = 4x - 3 Ditanya : Gradien garis "m"...?? Jawab : Karena yang diketahui adalah garis "n", maka kita cari dulu gradiennya. Tapi sebelumnya, silahkan baca dulu bagaimana mencari gradien suatu garis pada 2 artikel berikut ya!! Baca : Konsep umum mencari gradien suatu garis lurus Contoh soal mencari gradien garis lurus Setelah mengetahui cara mencari gradien suatu garis lurus, maka kita mampu menghitung gradien garis "n". y = 4x -3 Karena y tela

Setelah sebelumnya membahas persamaan garis yang tegak lurus, sekarang saya akan membahas bagaimana cara mencari persamaan garis yang sejajar. Baca pula : Mencari Gradien Garis L yg Tegak Lurus Garis 3x - y = 4 Mencari Gradien Garis K yg Tegak Lurus Dengan Garis 4x - 2y = 5 Prosesnya lebih gampang dibandingkan dengan persamaan garis lurus. Nanti akan dijelaskan lagi secara lebih jelas mengapa mencari persamaan garis seperti ini lebih enteng. Contoh soal  1. Suatu garis K melewati titik (2,3) serta sejajar dengan garis N yg mempunyai persamaan 2y + 3x = 4. Bagaimanakah persamaan garis K tersebut? Langkah buat mendapatkan jawaban menurut soal ini adalah : mencari gradien garis menurut 2y + 3x = 4 karena sejajar, maka gradien garis K sama menggunakan gradien garis N Setelah itu tambahkan datanya ke rumus persamaan garis. Nah, seperti itulah langkah-langkah yg sanggup kita tempuh. Mencari gradien garis N menggunakan persamaan 2y + 3x = 4. Untuk menerima gradiennya, maka y harus sendiri di

Untuk melihat perpaduan soal-soal tentang gradien garis, silahkan cek di link berikut ini : ====>>> "Kumpulan soal-soal gradien garis lurus" Ok, kini kita langsung masuk ke contoh soalnya : 1. Suatu garis lurus mempunyai persamaan 2x = 6y -4, berapakah gradien garisnya??? Jawab : Persamaan ini wajib diubah dahulu supaya memenuhi y = mx + c Variabel "y" pada persamaan diatas masih berada pada kanan tanda (=), maka wajib dipindah dahulu serta di depan variabel "y" nir boleh terdapat angka selain 1. Pada persamaan diatas, "y" sudah berada pada kiri (=) tapi masih ada nomor -6 disana. Jadi wajib dihilangkan menggunakan cara membaginya menggunakan -6 juga. Nah, variabel "y" sudah sendiri serta tidak ada nomor pada depannya (atau hanya terdapat nomor 1. Ingat 1y = y). Jadi gradien garis lurus persamaan diatas merupakan angka di depan variable "x", yaitu 1/3. gradien (m) = 1/3. Anda pula sanggup membaca konsep umum mengenai

Mencari gradien garis lurus sangatlah gampang sekali, bila anda mengerti konsep yg sebenarnya. Dan disini saya akan menunjukkan konsep mudah buat memeriksa materi ini. Ok, pribadi saja simak model dibawah ini ya!!   Misalnya ada persamaan garis menggunakan bentuk : "y = mx + a"  m = gradien dari garis lurus. Untuk menerima nilai dari gradien (m), ada beberapa syarat krusial yang sangat perlu anda ketahui. y harus sendiri berada disebelah kiri tanda sama menggunakan (=) serta tidak boleh ada yang menemaninya lagi tidak boleh ada angka dua, tiga 4 dan seterusnya di depan "y", lantaran hanya nomor 1 saja yg boleh. (ingat bahwa 1y = y) Setelah ke 2 kondisi diatas terpenuhi, maka gradien (m) adalah nomor di depan variable x.  Itulah gradien yang kita cari. Itulah konsep generik dalam mencari gradien suatu garis lurus. Untuk detail, silahkan baca lagi tentang model soal tentang gradien dalam bagian related post dibawah tulisan ini. semoga berguna ya!! Untuk lebih jelasny

Rumus Persamaan Garis Lurus Beserta Contoh Soal - Dalam pelajaran Matematika terdapat materi pembelajaran tentang rumus persamaan garis lurus. Apa itu persamaan garis lurus? Persamaan garis lurus tak jarang diklaim menjadi persamaan linier yg adalah persamaan yang terdiri dari satu variabel atau lebih. Persamaan garis lurus selalu berkaitan menggunakan gradien. Tanpa adanya gradien maka persamaannya tidak bisa diketahui, kecuali berpotongan antara kedua titik. Pada kesempatan kali ini aku akan menjelaskan mengenai rumus persamaan garis lurus beserta model soal persamaan garis lurus. Untuk detail dapat anda simak dibawah ini. Rumus Persamaan Garis Lurus Beserta Contoh Soal Persamaan garis lurus adalah perbandingan koordinat x menggunakan koordinat y yg yang terletak antara dua titik dalam garis. Dalam rumus persamaan garis lurus dan model soal persamaan garis lurus masih ada gradien didalamnya. Apa itu gradien? Gradien ialah perbandingan antara komponen x dengan komponen y yang akan

Dalam artikel ini, akan dibahas beberapa soal yg herbi cara mencari gradien suatu garis lurus apabila diketahui 2 buah titik. Ada satu rumus yg sanggup dipakai buat memecahkan permasalahan ini. Nah, nanti akan dibahas lebih mendalam lagi bagaimana cara menggunakan rumus dan mencari faktor-faktor yang terlibat pada dalamnya.. Ok, kita langsung ke model soalnya.. Contoh soal : 1. Sebuah garis lurus melalui titik (2,1) dan (4,dua). Berapakah gradien dari garis tersebut? Nah, mari kita perhatikan rumus buat mencari gradien berdasarkan dua buah titik. m merupakan gradien x₁ dan y₁ adalah nilai koordinat pada titik pertama x₂ dan y₂ adalah koordinat pada titik kedua Langkah pertama adalah menentukan titik-titiknya.. Titik pertama (dua,1) : x₁ = 2 y₁ = 1 Titik ke 2 (4,2) x₂ = 4 y₂ = 2 Ok, sekarang kita pribadi mencari gradiennya.. Nah, gradien yang dicari adalah (m) = ½ Bagaimana? Praktis sekali bukan? Yang krusial jangan sampai keliru menempatkan mana x₁, y₁ serta x₂, y₂.. Ingat koordinat t

Mencari gradien menurut suatu persamaan garis yg sudah diketahui mudah sekali. Yang penting tahu konsepnya, maka gradien bisa diperoleh. Nah, dibawah ini akan diberikan sedikit model soal bagaimana cara mencari gradien menurut suatu garis lurus yg diketahui persamaannya.. Contoh soal : 1. Garis "a" mempunyai persamaan 2x + y = 4. Berapakah gradien menurut garis a? Untuk mendapatkan gradien berdasarkan suatu garis lurus yang telah diketahui persamaannya, sanggup diperhatikan cara berikut.. Caranya : buat variabel "y" berada sendiri di sebelah kiri koefisien "y" haruslah 1 gradien merupakan angka pada depan variabel "x" Biar lebih dipahami, kita perhatikan contoh soalnya saja.. Persamaan garisnya adalah 2x + y = 4 y terdapat sahabat pada sebelah kiri, yaitu 2x 2x harus dipindahkan ke ruas kanan agar y sendiri pada ruas kiri 2x pindah sebagai akibatnya sebagai (-2x) 2x + y = 4 y = -2x + 4 Sekarang perhatikan apakah "y" koefisiennya telah

Garis lurus memang ditandakan sang adanya gradien atau kemiringannya. Dan kini kita akan membahas galat satu bentuk soal yg herbi gradien. Ini merupakan variasi lainnya. Mari lihat lagi soalnya.. Contoh soal : 1. Suatu garis lurus melewati titik (2,6) serta (1,a) serta garis ini memiliki gradien (m) = tiga. Berapakah nilai a? Langkah 1 → Analisa soal Yang diketahui hanyalah gradien garis bersama 2 titiknya. Jadi,, Soal misalnya ini hanya cukup diselesaikan menggunakan rumus gradien garis saat dilewati 2 butir titik. Masih jangan lupa rumus gradien garisnya? Langkah 2 → Mencari jawabannya Rumus buat mencari gradien adalah sebagai berikut. Bagaimana memilih nilai y dan x nya? Lihat lagi dibawah ini.. Jelas ya? Bagaimana apabila (1,a) digunakan menjadi x1 dan y1? Hasilnya sama saja.. Anda bebas menentukan mana yang pertama serta mana yg kedua.. Sekarang kita tambahkan ke rumusnya.. Ganti m menggunakan 3 Masukkan y2, y1, x2, x1 sesuai dengan yg sudah dijelaskan diatas. Untuk menghilangkan

Apabila suatu titik terletak dalam satu garis lurus, berarti ketiga titik itu berada dalam satu gradien yg sama. Nah, inilah dasar yg akan digunakan buat menjawab soal pada bentuk seperti ini. Ayo kita lihat lagi soalnya.. Soal  1. Tiga butir titik (1,3), (-2, -3) serta (a,9) terletak pada satu garis lurus. Berapakah nilai berdasarkan "a"? Diatas sudah dijelaskan jika tiga titik yg berada pada satu garis lurus akan memiliki gradien yang sama. Masih ingat cara mencari gradien menurut 2 titik? Untuk menerima gradien, maka kita memerlukan minimal 2 titik. Nah ayo kita lihat lagi caranya.. Titik pertama , (1,tiga) : x₁ = 1 y₁ = 3 Titik ke 2, (-dua, -tiga) : x₂ = -2 y₂ = -3 Titik ketiga, (a, 9) : x₃ = a y₃ = 9 Rumus buat gradien berdasarkan 2 titik serta yg akan digunakan dalam soal ini adalah : Kita masukkan pribadi masing-masing x serta y ke persamaan diatas, sebagai akibatnya mampu diperoleh nilai "a"-nya berapa. masukkan masing-masing nilai x dan y -6 dibagi dengan